题目内容
已知某黄金矩形的周长是(2
+2)cm,则它的面积是 cm2.
| 5 |
考点:黄金分割
专题:
分析:根据黄金矩形的宽与长的比为
,设长为xcm,则宽为
xcm,由黄金矩形的周长是(2
+2)cm,列出方程,解方程求出x的值,再根据矩形的面积=长×宽,代入数值计算即可求解.
| ||
| 2 |
| ||
| 2 |
| 5 |
解答:解:设黄金矩形的长为xcm,则宽为
xcm,
由题意得,2(x+
x)=2
+2,
解得x=2,
所以它的面积是:x•
x=2×
×2=2
-2(cm2).
故答案为(2
-2).
| ||
| 2 |
由题意得,2(x+
| ||
| 2 |
| 5 |
解得x=2,
所以它的面积是:x•
| ||
| 2 |
| ||
| 2 |
| 5 |
故答案为(2
| 5 |
点评:本题考查了黄金矩形的定义,矩形的周长与面积,设黄金矩形的长为xcm,根据黄金矩形的周长是(2
+2)cm列出方程是解题的关键.
| 5 |

练习册系列答案
相关题目
 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为EF,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
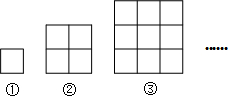 如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )
如图,每一幅图中均含有若干个正方形,第①幅图中含有1个正方形;第②幅图中含有5个正方形;按这样的规律下去,则第⑥幅图中含有正方形的个数为( )| A、55 | B、78 | C、91 | D、140 |
 如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC
如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC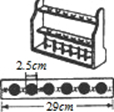 如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为
如图是学校化学实验室用于放试管的木架,在每层长29cm的木条上钻有6个圆孔,每个圆孔的直径均为2.5cm.两端与圆孔边缘及任何相邻两孔边缘之间的距离都相等并设为xcm,则x为 如图,回答下列问题:
如图,回答下列问题: