题目内容
 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
(1)求点A、B、C的坐标;
(2)若点P是直线l上的一个动点,在点P运动的过程中:
①当△PAC的周长最小时,点P的坐标为
②在①的情形下,以点A为圆心,AP的长为半径作⊙A,试说明BP是⊙A的切线;
(3)当△PAC为等腰三角形时,直接写出所有符合条件的点P的坐标.
考点:二次函数综合题
专题:
分析:(1)令y=0即可求出A,B的坐标,令x=0即可求出点C的坐标.
(2)①先求出AE所在的直线解析式,与l的交点就是点P的坐标,②连接AP,先求出∠PAD=45°,由PD是AB的垂直平分线,得出∠PBA=45°,得出∠APB=90°,即可得出BP是⊙A的切线;
(3)△PAC为等腰三角形分为三种情况)①当AC=AP时,△PAC为等腰三角形,②当AC=CP时,△PAC为等腰三角形,③当CP=AP时,△PAC为等腰三角形,分别求出点P的坐标.
(2)①先求出AE所在的直线解析式,与l的交点就是点P的坐标,②连接AP,先求出∠PAD=45°,由PD是AB的垂直平分线,得出∠PBA=45°,得出∠APB=90°,即可得出BP是⊙A的切线;
(3)△PAC为等腰三角形分为三种情况)①当AC=AP时,△PAC为等腰三角形,②当AC=CP时,△PAC为等腰三角形,③当CP=AP时,△PAC为等腰三角形,分别求出点P的坐标.
解答:解:(1)令-
x2+x+4=0,解得x1=-2,x2=4,
∴A的坐标为(-2,0),点B的坐标为(4,0),
令x=0,解得y=4,
∴点C的坐标为(0,4).
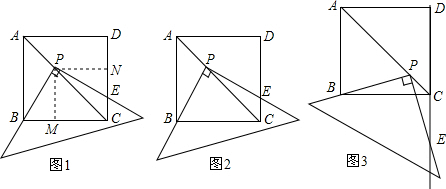
(2)①如图1,过点C作CE⊥l与抛物线交于点E,连接AE交l于点于点P,此时△PAC的周长最小

设AE所在的直线解析式为y=kx+b,
∵点C的坐标为(0,4),对称轴l=1,
∴点E的坐标为(2,4),
∴点A的坐标为(-2,0),
解得
.
∴AE所在的直线解析式为y=x+2,
∵l=1,
∴y=1+2=3,
所以点P的坐标为(1,3),
故答案为:(1,3).
②如图2,连接AP,

∵点P(1,3),
∴PD=3,
∵A(-2,0),l=1,
∴AD=3,
∵∠PDA=90°,
∴∠PAD=∠APD=45°,
∵PD是AB的垂直平分线,
∴AP=BP,
∴∠PAB=∠PBA=45°,
∴∠APB=90°,
∴BP是⊙A的切线;
(3)①如图3,当AC=AP时,△PAC为等腰三角形,

设P(1,y),则AP=
=
,
∵AC=
=
=
∴
=
,
∴y=±
,
∴P(1,
)或(1,-
).
②如图4,当AC=CP时,△PAC为等腰三角形,

设P(1,y),
∵C(0,3),
∴CP=
,
∵AC=
=
=
∴
=
,
∴y=3±
,
∴点P的坐标为(1,3+
)或(1,3-
)
③如图5,当CP=AP时,△PAC为等腰三角形,

设P(1,y),
∵C(0,3),A(-2,0)
∴CP=
,
AP=
∵AC=AP
∴
=
,
∴y=
,
∴点P的坐标为(1,
).
∴当△PAC为等腰三角形时,点P的坐标为:(1,
)或(1,-
)或(1,3+
)或(1,3-
)或(1,
).
| 1 |
| 2 |
∴A的坐标为(-2,0),点B的坐标为(4,0),
令x=0,解得y=4,
∴点C的坐标为(0,4).
(2)①如图1,过点C作CE⊥l与抛物线交于点E,连接AE交l于点于点P,此时△PAC的周长最小

设AE所在的直线解析式为y=kx+b,
∵点C的坐标为(0,4),对称轴l=1,
∴点E的坐标为(2,4),
∴点A的坐标为(-2,0),
|
解得
|
∴AE所在的直线解析式为y=x+2,
∵l=1,
∴y=1+2=3,
所以点P的坐标为(1,3),
故答案为:(1,3).
②如图2,连接AP,

∵点P(1,3),
∴PD=3,
∵A(-2,0),l=1,
∴AD=3,
∵∠PDA=90°,
∴∠PAD=∠APD=45°,
∵PD是AB的垂直平分线,
∴AP=BP,
∴∠PAB=∠PBA=45°,
∴∠APB=90°,
∴BP是⊙A的切线;
(3)①如图3,当AC=AP时,△PAC为等腰三角形,

设P(1,y),则AP=
| AD2+DP2 |
| 9+y2 |
∵AC=
| AO2+OC2 |
| 22+42 |
| 20 |
∴
| 9+y2 |
| 20 |
∴y=±
| 11 |
∴P(1,
| 11 |
| 11 |
②如图4,当AC=CP时,△PAC为等腰三角形,

设P(1,y),
∵C(0,3),
∴CP=
| (y-3)2+12 |
∵AC=
| AO2+OC2 |
| 22+42 |
| 20 |
∴
| (y-3)2+12 |
| 20 |
∴y=3±
| 19 |
∴点P的坐标为(1,3+
| 19 |
| 19 |
③如图5,当CP=AP时,△PAC为等腰三角形,

设P(1,y),
∵C(0,3),A(-2,0)
∴CP=
| (y-3)2+12 |
AP=
| y2+32 |
∵AC=AP
∴
| (y-3)2+12 |
| y2+32 |
∴y=
| 1 |
| 6 |
∴点P的坐标为(1,
| 1 |
| 6 |
∴当△PAC为等腰三角形时,点P的坐标为:(1,
| 11 |
| 11 |
| 19 |
| 19 |
| 1 |
| 6 |
点评:本题主要考查了二次函数的综合题,本题的难点是(3)解题的关键是分三种情况讨论△PAC为等腰三角形时点P的坐标.

练习册系列答案
相关题目
 如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.
如图,O是直线AB上一点,∠BOC=3∠AOC,OC是∠AOD的平分线.