Question

如图，△ABC中，E、D是BC边上的三等分点，F是AC的中点，BF交AD、AE于G，H，试求BG：GH：HF．

Answer 1

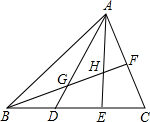
过F作FN∥BC，交AE于M，AD于N，
∵F为AC中点，
∴FM是△AEC中位线，
∴MF=

1

2

CE，CE=2FM，
∵BD=DE=CE，
∴BE=2CE=4FM，
∵FM∥BC，
∴△FMH∽△BEH，
∴

FH

BH

=

FM

BE

=

1

4

，
∵FN是△ADC的中位线，
∴FN=

1

2

CD=CE=BD，
∵FN∥BC，
∴△FNG∽△BDG，
∴

BG

GF

=

BD

FN

=

1

1

，
∴BG=GF，
∵

FH

BH

=

1

4

，
∴

FH

BF

=

1

5

，
∴FH=

1

5

BF，
∵BG=

1

2

BF，HF=

1

5

BF，
∴GH=GF-HF=

1

2

BF-

1

5

BF=

3

10

BF，
∴BG：GH：HF=（

1

2

BF）：（

3

10

BF）：（

1

5

BF）=5：3：2．