题目内容
11.如图的数阵由奇数按规律排列而成,用一个十字框架每次框出5个数.(1)若将十字形框架中心位置的数记为a,则框架中的上、下、左、右四个数依次是a-16、a+16、a-2、a+2.
(2)经过计算说明这5个数的和可以是3000吗?可以是425吗?
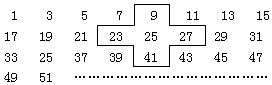
(3)这五个数的和可以是1844325吗?为什么?
分析 (1)根据中间数a左右相邻的两个数相差2,上下相邻的两个数相差16,进而填空;
(2)根据和为3000、425列出方程求得a的值,根据数列为奇数且第n行的第一个数为16n-15和最后一个数为16n-1检验是否符合题意.
(3)与(2)同理可得.
解答 解:(1)根据图中数据可知,中间数a左右相邻的两个数相差2,上下相邻的两个数相差16,
即a-16;a+16;a-2;a+2,
故答案为a-16;a+16;a-2;a+2;
(2)根据题意得:a-16+a+16+a-2+a+2=3000,即5a=3000,
解得:a=600,不是奇数,
∴这5个数的和不会是3000;
若5a=425,则a=85,
∵第n行的第一个数为1+16(n-1)=16n-15,最后一个数为15+16(n-1)=16n-1,
∴当16n-15=85时,n=6.25,不是整数;
当16n-1=85时,n=5.375,不是整数;
∴85不是第一个又不是最后一个,
∴这5个数的和可以是425;
(3)根据题意得:5a=1844325,
解得:a=368865,
∵当16n-15=368865时,n=23055,是整数,
即368865是第23055行第1个数,
故这五个数的和不可能是1844325.
点评 本题考查一元一次方程的应用,关键是看到表格中中间位置的数和四周数的关系,最后可列出方程求解.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
16.如果a+b=c,且a、b都大于c,那么a、b一定是( )
| A. | 同为负数 | B. | 一个正数一个负数 | ||
| C. | 同为正数 | D. | 一个负数一个是零 |
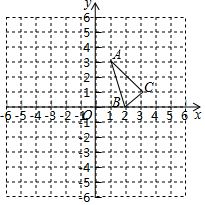 如图,把△ABC向下平移2个单位长度,再向左平移4个单位长度得△A′B′C′,解答下列各题.
如图,把△ABC向下平移2个单位长度,再向左平移4个单位长度得△A′B′C′,解答下列各题.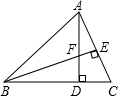 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=45°.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D,E,AD与BE相交于点F,若BF=AC,则∠ABC=45°.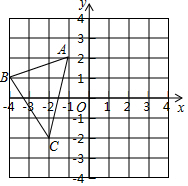 如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).
如图,已知△ABC的三个顶点的坐标为A(-1,2),B(-4,1),C(-2,-2).