题目内容
如图,在平面直角坐标系中,直线




















(1)当点




(2)在运动过程中,①当点





(3)作点









练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
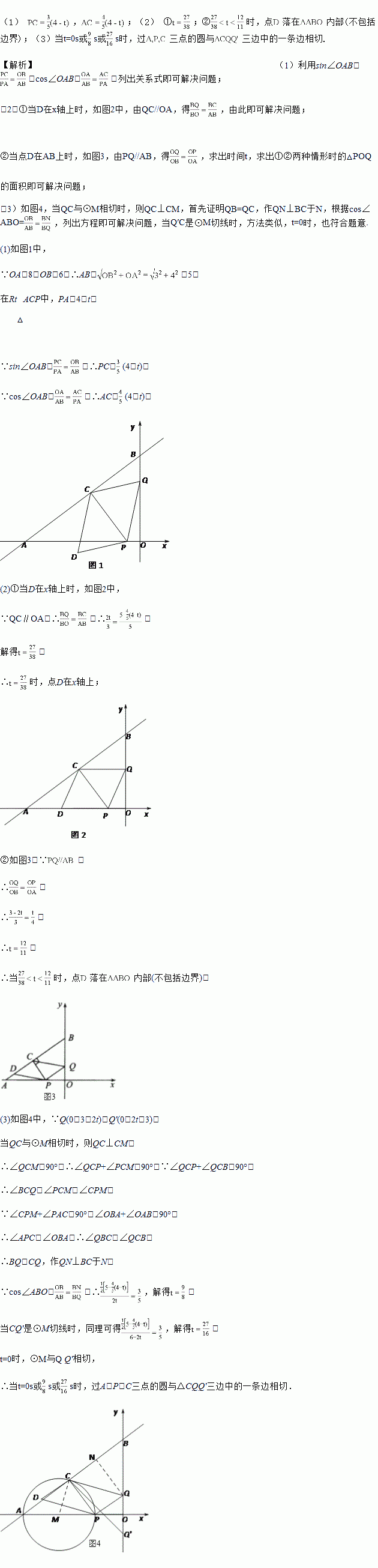

 B.
B.  C.
C.  D.
D. 

 ,1.010010001.(每两个1中多一个0),
,1.010010001.(每两个1中多一个0),  ,π,
,π,  中,则无理数有( )
中,则无理数有( )









 、
、 ,若回到
,若回到 ________(结果保留根号).
________(结果保留根号).

 B.
B.  C.
C.  D.
D. 