题目内容
 一辆卡车装满货物后,它的高比宽多1.5米,且恰好通过如图所示的隧道(上部为半圆形),求卡车的高度.
一辆卡车装满货物后,它的高比宽多1.5米,且恰好通过如图所示的隧道(上部为半圆形),求卡车的高度.考点:垂径定理的应用,勾股定理
专题:
分析:作弦EF∥AD,OH⊥EF于H,连接OF,在直角△OFH中,根据三角函数就可以求出OH,求出隧道的高,就可以判断.
解答: 解:设该卡车的宽是x米,高是(x+1.5)米.
解:设该卡车的宽是x米,高是(x+1.5)米.
如图,设半圆O的半径为R,则R=2.5米,
作弦EF∥AD,且EF=x米,OH⊥EF于H,
连接OF,
由OH⊥EF,得HF=
x米,
在Rt△OHF中,OH=
=
米,
则OH+4=x+1.5,即
+4=x+1.5,
整理得 x2-4x=0,
解得 x1=0(舍去),x2=4.
则该卡车的高度为:4+2=6(米).
答:卡车的高度大约是6m.
 解:设该卡车的宽是x米,高是(x+1.5)米.
解:设该卡车的宽是x米,高是(x+1.5)米.如图,设半圆O的半径为R,则R=2.5米,
作弦EF∥AD,且EF=x米,OH⊥EF于H,
连接OF,
由OH⊥EF,得HF=
| 1 |
| 2 |
在Rt△OHF中,OH=
| OF2-HF2 |
2.52-
|
则OH+4=x+1.5,即
2.52-
|
整理得 x2-4x=0,
解得 x1=0(舍去),x2=4.
则该卡车的高度为:4+2=6(米).
答:卡车的高度大约是6m.
点评:本题考查了垂径定理及勾股定理的应用,本题的关键是建立数学模型,善于观察题目的信息是解题以及学好数学的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
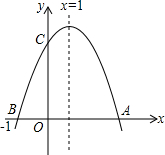 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①ac<0;②a+b+c<0;③b2-4ac>0;④若(-5,y1),(
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①ac<0;②a+b+c<0;③b2-4ac>0;④若(-5,y1),(| 5 |
| 2 |
| A、①③④ | B、②③④ |
| C、②③④ | D、①③ |
下列各方程中,哪些是一元一次方程?( )
①4x-3=x;②3x(x-2)=1;③1-2a=2a+1;④3a2=5;⑤
=3x-2;⑥x+1=
;⑦2x-6y=3x-1;⑧x=1.
①4x-3=x;②3x(x-2)=1;③1-2a=2a+1;④3a2=5;⑤
| 2x+4 |
| 3 |
| 1 |
| x |
| A、①③ | B、①③⑤ |
| C、⑤⑥ | D、①③⑤⑧ |
下列说法正确的是( )
| A、有理数和数轴上的点一一对应 | ||||||
| B、立方根等于本身的数只有±1 | ||||||
| C、(-2)2的算术平方根是-2 | ||||||
D、-
|
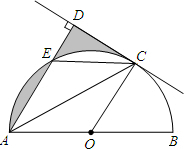 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE. 如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是
如图,是一个正方体的表面展开图,则原正方体中“国”字所在的面相对的面上标的字是