题目内容
如图,平行四边形ABCD中,E为AD延长线上的一点,D为AE的一个黄金分割点,即AD= AE,BE交DC于点F.若CF=2,则AB的长为 .
AE,BE交DC于点F.若CF=2,则AB的长为 .

 +1
+1
【解析】
先由AD= AE,得出DE=
AE,得出DE= AE,再根据平行四边形的性质得出DF∥AB,DC=AB,从而得出△EDF∽△EAB,根据相似三角形比例关系即可得出答案.
AE,再根据平行四边形的性质得出DF∥AB,DC=AB,从而得出△EDF∽△EAB,根据相似三角形比例关系即可得出答案.
【解析】
∵AD= AE,
AE,
∴DE= AE.
AE.
∵四边形ABCD为平行四边形,
∴DF∥AB,DC=AB,
∴△EDF∽△EAB,
∴ =
= ,
,
∴ =
= ,
,
解得AB= +1.
+1.
故答案为: +1.
+1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



 那么
那么 等于( )
等于( )

 ,
, ,用
,用 、
、 表示向量
表示向量 正确的是( )
正确的是( ) B.
B. C.
C.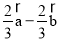 D.
D.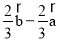
 与
与 的方向相反,且
的方向相反,且 ,
, ,则下列用
,则下列用 B.
B. C.
C. D.
D.