题目内容
如图,AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,p是直线CD上的一个动点,(点P不与F重合)

(1)当点P在射线FC上移动时,如图(1),∠FMP+∠FPM=∠AEF成立吗?请说明理由.
(2)当点P在射线FD上移动时,如图(2),∠FMP+∠FPM与∠AEF有什么关系?说明你的理由.

(1)当点P在射线FC上移动时,如图(1),∠FMP+∠FPM=∠AEF成立吗?请说明理由.
(2)当点P在射线FD上移动时,如图(2),∠FMP+∠FPM与∠AEF有什么关系?说明你的理由.
分析:(1)由AB∥CD,利用两直线平行,同旁内角互补,可得∠AEF十∠EFC=180°,又由三角形内角和定理,即可得∠FMP+∠FPM+∠EFC=180°,则可得∠FMP+∠FPM=∠AEF;
(2)由AB∥CD,利用两直线平行,内错角相等,即可证得∠AEF=∠EFD,又由三角形内角和定理,即可得∠FMP+∠FPM+∠EFD=180°,则可得∠FMP+∠FPM+∠AEF=180°.
(2)由AB∥CD,利用两直线平行,内错角相等,即可证得∠AEF=∠EFD,又由三角形内角和定理,即可得∠FMP+∠FPM+∠EFD=180°,则可得∠FMP+∠FPM+∠AEF=180°.
解答:解:(1)成立.…(2分)
理由:∵AB∥CD,
∴∠AEF十∠EFC=180°(两直线平行,同旁内角互补),
∵∠FMP+∠FPM+∠EFC=180°(三角形内角和定理),
∴∠FMP+∠FPM=∠AEF(等量代换); …(6分)
(2)∠FMP+∠FPM与∠AEF互补(或∠FMP+∠FPM+∠AEF=180°)…(8分)
理由:∵AB∥CD,
∴∠AEF=∠EFD(两直线平行,内错角相等),
∵∠FMP+∠FPM+∠EFD=180°(三角形内角和定理),
∴∠FMP+∠FPM+∠AEF=180°(等量代换). …l2
理由:∵AB∥CD,
∴∠AEF十∠EFC=180°(两直线平行,同旁内角互补),
∵∠FMP+∠FPM+∠EFC=180°(三角形内角和定理),
∴∠FMP+∠FPM=∠AEF(等量代换); …(6分)
(2)∠FMP+∠FPM与∠AEF互补(或∠FMP+∠FPM+∠AEF=180°)…(8分)
理由:∵AB∥CD,
∴∠AEF=∠EFD(两直线平行,内错角相等),
∵∠FMP+∠FPM+∠EFD=180°(三角形内角和定理),
∴∠FMP+∠FPM+∠AEF=180°(等量代换). …l2
点评:此题考查了平行线的性质与三角形内角和定理.此题难度适中,注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,注意数形结合思想的应用.

练习册系列答案
相关题目
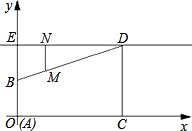 横坐标为x,纵坐标为y.
横坐标为x,纵坐标为y. 如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
