题目内容
16. 如图,BD为正方形ABCD的对角线,点G是CD延长线上一点,连接AG,过AG上的点E作EF⊥AG交BD于点F,连接GF,已知EG=EB.
如图,BD为正方形ABCD的对角线,点G是CD延长线上一点,连接AG,过AG上的点E作EF⊥AG交BD于点F,连接GF,已知EG=EB.(1)若EB=3,BG=2,求DB的长度.
(2)证明:EF=BE.
分析 (1)在RT△AGB中,由EG=EB可以证明E是AG中点,进而可以求出AG,AB,BD的长度.
(2)连接AF,FC可以证明∠AFG=90°,根据直角三角形斜边中线定理EF=$\frac{1}{2}$AG,EB=$\frac{1}{2}$AG,可以得到结论.
解答 (1)解:∵BE=GE,
∴∠EBG=∠EGB,
∵∠EBG+∠EBA=90°,∠AGB+∠GAB=90°,
∴∠EBA=∠EAB,
∴EA=EB,
∴AG=2BE=6,
∵GB=2,
∴AB=$\sqrt{{6}^{2}-{2}^{2}}$
=4$\sqrt{2}$
∴BD=$\sqrt{2}$AB=$\sqrt{2}$×$4\sqrt{2}$=8.
(2)证明:连接AF,FC,
由(1)可知AE=GE,EF⊥AG,
∴AF=FG,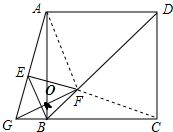
∵四边形ABCD是正方形,BD是对角线,
∴∠HBF=∠IBF=45°,
∵AB=CB,BF=BF,
∴△ABF≌△CBF,
∴FA=FC=FG,
∴∠BAF=∠BCF=∠FGC,
∵∠GOB+∠OGB=90°,∠AOF=∠GOB,
∴∠OAF+∠AOF=90°,
∴∠AFG=90°,
∵AE=EG,∴EF=$\frac{1}{2}$AG,∵EB=$\frac{1}{2}$AG,
∴EF=EB.
点评 本题目考查了正方形的性质,直角三角形的斜边中线定理,全等三角形的等知识.利用斜边中线等于斜边的一半,是解决EF=EB的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
6.如果|5-a|+|b+3|=0,则代数式$\frac{b}{a+b}$的值( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
7.x是一个三位数,现把4放在它的右边组成一个新的四位数是( )
| A. | 10x+4 | B. | 100x+4 | C. | 1000x+4 | D. | x+4 |
11. 如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
 如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )
如图,已知数轴上的点A、B、O、C、D、E分别表示数-3、-2、0、1、2、3,则表示数-1+$\sqrt{5}$的点P应落在线段( )| A. | AB上 | B. | OC上 | C. | CD上 | D. | DE上 |
1.已知关于x的方程x2-2x-2n=0有两个不相等的实数根,若n<5,且方程的两个实数根都是整数,则n的值为( )
| A. | n=2 | B. | n=0或n=1.5或n=4 | C. | n=4 | D. | n=0或n=1.5或n=2 |
5.下列图形或几何体中,投影可能是线段的是( )
| A. | 正方形 | B. | 长方体 | C. | 圆锥 | D. | 圆柱 |
 根据图中提供的信息,可知一把暖瓶的价格是35.
根据图中提供的信息,可知一把暖瓶的价格是35. 如图,是一个几何体的侧面展开图.
如图,是一个几何体的侧面展开图.