Question

13．如图，已知平行四边形ABCD，点E在AB的延长线上，连接BE、DE，过点D作DF∥EB交CA的延长线于点F，连接FB
（1）求证：△DAF≌△BCE；
（2）如果四边形ABCD是菱形，求证：四边形BEDF是菱形．

Answer 1

分析 （1）由平行四边形的性质得出AD=CB，AD∥CB，证出∠DAF=∠BCE，∠DFA=∠BEC，由AAS证明△DAF≌△BCE即可；
（2）先证明四边形BEDF是平行四边形，再由菱形的性质得出AC⊥BD，即可得出四边形BEDF是菱形．

解答 （1）证明：∵四边形ABCD是平行四边形，
∴AD=CB，AD∥CB，
∴∠DAC=∠BCA，
∴∠DAF=∠BCE，
∵DF∥EB，
∴∠DFA=∠BEC，
在△DAF和△BCE中，
$\left\{\begin{array}{l}{∠DAF=∠BCE}&{\;}\\{∠DFA=∠BEC}&{\;}\\{AD=CB}&{\;}\end{array}\right.$，
∴△DAF≌△BCE（AAS）；
（2）证明：连接BD，如图所示：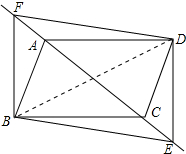
由（1）得：△DAF≌△BCE，
∴DF=BE，
又∵DF∥BE，
∴四边形BEDF是平行四边形，
∵四边形ABCD是菱形，
∴AC⊥BD，
即EF⊥BD，
∴四边形BEDF是菱形．

点评 本题考查了菱形的判定与性质、平行四边形的性质、全等三角形的判定与性质；熟练掌握平行四边形的性质，并能进行推理论证是解决问题的关键．