题目内容
已知点C、D是线段AB的两个黄金分割点,若CD=5,则AB= .
考点:黄金分割
专题:计算题
分析:根据黄金分割的定义得到AD=
AB,则AC=AB-AD=
AB,再利用AD-AC=CD得到(
-1)AB=5,然后利用分母有理化计算出AB.
| ||
| 2 |
3-
| ||
| 2 |
| 5 |
解答:解:如图,
∵点C、D是线段AB的两个黄金分割点,
∴AD=
AB,
∴AC=AB-AD=
AB,
∴AD-AC=
AB-
AB=(
-1)AB=CD,
∴(
-1)AB=5,
∴AB=
.
故答案为
.

∵点C、D是线段AB的两个黄金分割点,
∴AD=
| ||
| 2 |
∴AC=AB-AD=
3-
| ||
| 2 |
∴AD-AC=
| ||
| 2 |
3-
| ||
| 2 |
| 5 |
∴(
| 5 |
∴AB=
5
| ||
| 4 |
故答案为
5
| ||
| 4 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点;其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
下列事件是必然事件的是( )
| A、阴天一定会下雨 |
| B、在装有5个红球的袋中摸出1个球,是红球 |
| C、打开电视机,正在播放动画片 |
| D、某彩票中奖率是1%,买100张一定会中奖 |
下列说法正确的是( )
| A、三角形两边之差大于第三边 |
| B、所有的等边三角形都是全等的 |
| C、有两个角互余的三角形是直角三角形 |
| D、正n边形的内角和为180°n-2 |
下列图形既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
如果
是二次根式,那么a应满足( )
| a-3 |
| A、a≥0 | B、a≠3 |
| C、a=3 | D、a≥3 |
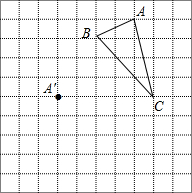 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A′,点B′、C′分别是B、C的对应点.