题目内容
如图，若正方体的边长为a，M是AB的中点，则图中阴影部分的面积为分析：AC，DM交于点O，连接BO，可以证明△OAD≌△OAB，又∵△OAD和△OCM面积相等，∴图中阴影部分面积可以转化为△OAD和△OAB的面积．
解答：
解：找到CD的中点N，连接BN．
正方形ABCD中，AC为BD的垂直平分线，∴OB=OD，
∵在△OAD和△OAB中，AB=AD，OA=OA
∴△OAD≌△OAB，
又∵S△AMD=S△AMC=
× AM×AD，
所以阴影部分面积为△OAD和△OAB的面积和．
根据中位线定理M、N分别为AB、CD的中点，
∴CE=EO=OA，∴O到AD的距离为CD长度的
．
∴S△ADO+S△ABO=2S△ADO=2×
×a×
a=
a2．
故答案为
a2．
解：找到CD的中点N，连接BN．正方形ABCD中，AC为BD的垂直平分线，∴OB=OD，
∵在△OAD和△OAB中，AB=AD，OA=OA
∴△OAD≌△OAB，
又∵S△AMD=S△AMC=
| 1 |
| 2 |
所以阴影部分面积为△OAD和△OAB的面积和．
根据中位线定理M、N分别为AB、CD的中点，
∴CE=EO=OA，∴O到AD的距离为CD长度的
| 1 |
| 3 |
∴S△ADO+S△ABO=2S△ADO=2×
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
故答案为
| 1 |
| 3 |
点评：本题考查中位线定理的灵活应用，以及正方形对角线垂直平分，本题证明CE=EO=OA是解题的关键．
练习册系列答案
相关题目
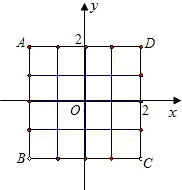3，4，5，6，连续抛掷两次，朝上的数字分别作为点P的坐标（第一次的点数为横坐标，第二次的点数为纵坐标）．
如图，若正方体的边长为a，M是AB的中点，则图中阴影部分的面积为________．
3，4，5，6，连续抛掷两次，朝上的数字分别作为点P的坐标（第一次的点数为横坐标，第二次的点数为纵坐标）．
？若存在，指出其中的一种平移方式；若不存在，请说明理由．
？若存在，指出其中的一种平移方式；若不存在，请说明理由。