Question

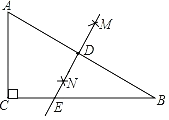
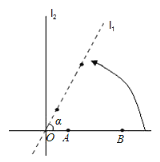
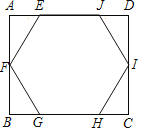
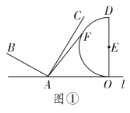
【题目】如图①，已知点、在直线上，且于点，且，以为直径在的左侧作半圆于点，且．

（1）若半圆上有一点，则的最大值为__________；

（2）向右沿直线平移得到．

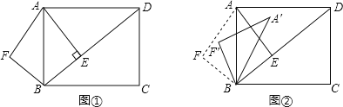
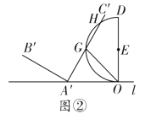
①如图②，若截半圆的的长为，求的度数；

②当半圆与的边相切时，求平移距离．

Answer 1

【答案】（1）；（2）①75°；②10－或2＋

【解析】

（1）连接AD，易知当点F与点D重合时，AF最大，然后利用勾股定理求出结论；

（2）①连接EG、EH，根据弧长公式即可求出∠GEH，从而证出△EGH为等边三角形，然后求出∠EGH=60°，可得，然后根据平行线的性质、等边对等角求出∠EGO即可求出结论；

②根据与半圆相切和与半圆相切分类讨论，然后分别画出图形，根据切线的性质和勾股定理求出，从而求出平移距离．

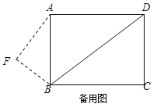
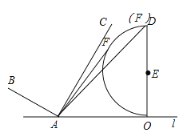
解：（1）连接AD，易知当点F与点D重合时，AF最大

∵，

∴AD=

即AF的最大值即为

故答案为：;

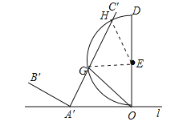
（2）①连接EG、EH

∵的长为，

∴∠GEH=×180°÷=60°

∵EG=EH

∴△EGH为等边三角形

∴∠EGH=60°

∴

∵

∴∠EGH=

∴GE∥直线l

∴∠GED=

∵EG=EO

∴∠EGO=∠EOG=

∴=－∠EGO=75°

②当与半圆相切时，切点为P，连接、PE

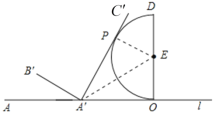
∴EP⊥，EO⊥直线l，EP=EO

∴平分∠

∴∠=∠=30°

在Rt△中，=

∴平移距离=AO－=10－；

当与半圆相切时，切点为P，连接EP并延长交直线l于点F，连接

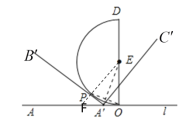
∴∠EPA′=∠FPA′=90°，A′O=A′P

∵，

∴∠=180°－－=30°

∴∠PFA′=60°，cos∠=

∴

在Rt△OFE中，OF=

∵

∴

解得：

∴平移距离=AO－=2＋

综上：平移距离为10－或2＋．