题目内容
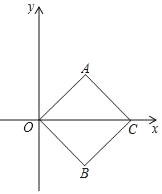
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() .若正方形
.若正方形![]() 绕点
绕点![]() 顺时针旋转,得正方形
顺时针旋转,得正方形![]() ,记旋转角为
,记旋转角为![]() .
.
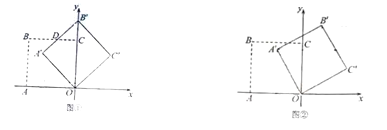
(Ⅰ)如图①,当![]() 时,求
时,求![]() 与
与![]() 的交点
的交点![]() 的坐标;
的坐标;
(Ⅱ)如图②,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(Ⅲ)若![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 长的取值范围(直接写出结果即可)。
长的取值范围(直接写出结果即可)。
【答案】(Ⅰ)![]() 的坐标为
的坐标为![]() ;(Ⅱ)点
;(Ⅱ)点![]() 的坐标为
的坐标为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)当α=45°时,则![]() ,点
,点![]() 在y轴上,根据勾股定理可得
在y轴上,根据勾股定理可得![]() 的长,再根据Rt△
的长,再根据Rt△![]() 为等腰直角三角形,可得
为等腰直角三角形,可得![]() ,从而得出点D的坐标;
,从而得出点D的坐标;
(Ⅱ)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() . 当
. 当![]() 时,可证得
时,可证得![]() ,再利用直角三角形中
,再利用直角三角形中![]() 所对的直角边是斜边的一半和勾股定理,求出OD和
所对的直角边是斜边的一半和勾股定理,求出OD和![]() ,同理可求出
,同理可求出![]() 的长,从而得出点B′的坐标;
的长,从而得出点B′的坐标;
(Ⅲ)连接OB,AC相交于点K,则K是OB的中点,因为P为线段BC′的中点,所以PK=![]() OC′=3,即点P在以K为圆心,3为半径的圆上运动,即可得出AP长的取值范围.
OC′=3,即点P在以K为圆心,3为半径的圆上运动,即可得出AP长的取值范围.
解:(Ⅰ)∵点![]() ,点
,点![]() ,
,![]() 为正方形,
为正方形,
∴![]() ,
,![]() .
.
∵正方形![]() 是正方形
是正方形![]() 旋转得到的,
旋转得到的,
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
(Ⅱ)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() .
.

∵![]() ,
,![]()
∴![]() .
.
∵![]() ,
,![]() =6
=6
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
, ![]() , ∴
, ∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
(Ⅲ)![]() .
.

如图③,连接OB,AC相交于点K,
则K是OB、AC的中点,
∵P为线段BC′的中点,
∴PK=![]() OC′=3,AK=
OC′=3,AK=![]()
∴P在以K为圆心,3为半径的圆上运动,
∴AP最大值为AK+KP=![]() ,AP的最小值为AK-KP=
,AP的最小值为AK-KP=![]() ,
,
∴AP长的取值范围为:![]() .
.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案【题目】甲、乙施工队分别从两端修一段长度为380米的公路.在施工过程中,乙队曾因技术改进而停工一天,之后加快了施工进度并与甲队共同按期完成了修路任务.下表是根据每天工程进度绘制而成的.
施工时间/天 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
累计完成施工量/米 | 35 | 70 | 105 | 140 | 160 | 215 | 270 | 325 | 380 |
下列说法错误的是( )
A. 甲队每天修路20米
B. 乙队第一天修路15米
C. 乙队技术改进后每天修路35米
D. 前七天甲,乙两队修路长度相等
【题目】今年5月15日,亚洲文明对话大会在北京开幕.为了增进学生对亚洲文化的了解,某学校开展了相关知识的宣传教育活动。为了解这次宣传活动的效果,学校从全校1200名学生中随机抽取100名学生进行知识测试(测试满分100分,得分均为整数),并根据这100人的测试成绩,制作了如下统计图表。
100名学生知识测试成绩的频数表
成绩 | 频数(人) |
| 10 |
| 15 |
|
|
| 40 |
| 15 |
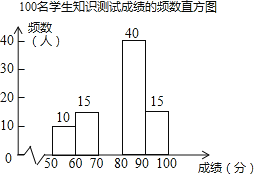
由图表中给出的信息回答下列问题:
(1)![]() ________,并补全额数直方图________;
________,并补全额数直方图________;
(2)小明在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由;
(3)如果80分以上(包括80分)为优秀,请估计全校1200名学生中成绩优秀的人数.
【题目】我市自开展“学习新思想,做好接班人”主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7及以上 |
人数(人) | 20 | 28 | m | 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果估计该校学生在这一周内文章阅读的篇数为4篇的人数.
【题目】某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数/人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |
频数分布表
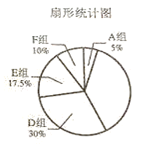
请根据图表中的信息解答下列问题:
(1)求频数分布表中m的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。