Question

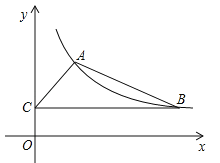
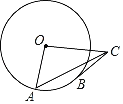
【题目】如图，⊙O的半径OA＝2，B是⊙O上的动点（不与点A重合），过点B作⊙O的切线BC，BC＝OA，连结OC，AC．当△OAC是直角三角形时，其斜边长为__．

Answer 1

【答案】2

【解析】

先根据切线的性质和等腰直角三角形的判定方法证得△OBC是等腰直角三角形，当 AOC＝90°，连接OB，根据勾股定理可得斜边AC的长，当 OAC＝90°，A与B重合，不符合题意．

解：连接OB，

∵BC是⊙O的切线，

∴∠OBC＝90°，

∵BC＝OA，

∴OB＝BC＝2，

∴△OBC是等腰直角三角形，

∴∠BCO＝45°，

∴∠ACO≤45°，

当∠AOC＝90°，△OAC是直角三角形时，

∴OC＝OB＝2，

∴AC＝＝＝2；

当 OAC＝90°，A与B重合，不符合题意，故排除此种情况；

∴其斜边长为2，

故答案为：2．