Question

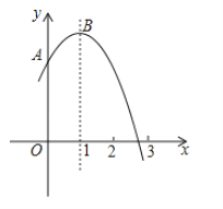
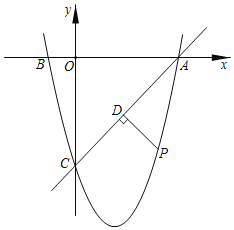
【题目】如图，在平面直角坐标系中，已知点的坐标为，且，抛物线图象经过三点．

（1）求两点的坐标；

（2）求抛物线的解析式；

（3）若点是直线下方的抛物线上的一个动点，作于点，当的值最大时，求此时点的坐标及的最大值．

Answer 1

【答案】（1）A（4，0）,C（0，﹣4）；（2） ；（3）PD的最大值为，此时点P（2，﹣6）．

【解析】

（1）OA＝OC＝4OB＝4，即可求解；

（2）抛物线的表达式为： ，即可求解；

（3），即可求解．

解：（1）OA＝OC＝4OB＝4，

故点A、C的坐标分别为（4，0）、（0，﹣4）；

（2）抛物线的表达式为：，

即﹣4a＝﹣4，解得：a＝1，

故抛物线的表达式为： ；

（3）直线CA过点C，设其函数表达式为：，

将点A坐标代入上式并解得：k＝1，

故直线CA的表达式为：y＝x﹣4，

过点P作y轴的平行线交AC于点H，

∵OA＝OC＝4，

，

∵

，

设点 ，则点H（x，x﹣4），

∵ ＜0，∴PD有最大值，当x＝2时，其最大值为，

此时点P（2，﹣6）．