题目内容
9．
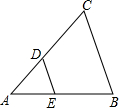如图，△ABC中，DE∥BC，AE：EB=2：3，则DE：BC=2：5．
分析 根据相似三角形的判定得出△ADE∽△ACB，根据相似三角形的性质得出$\frac{DE}{BC}$=$\frac{AE}{AB}$，求出AE：AB即可．
解答 解：∵AE：EB=2：3，
∴AE：AB=2：5，
∵DE∥BC，
∴△ADE∽△ACB，
∴$\frac{DE}{BC}$=$\frac{AE}{AB}$=$\frac{2}{5}$，
故答案为：2：5．
点评 本题考查了相似三角形的性质和判定的应用，能根据相似三角形的性质得出$\frac{DE}{BC}$=$\frac{AE}{AB}$是解此题的关键．
练习册系列答案
相关题目
19．下列语句中，是真命题的是（ ）
| A． | 任何实数都有相反数、倒数 | |
| B． | 过一点有且只有一条直线与已知直线平行 | |
| C． | 在同一平面内不相交的两条直线叫做平行线 | |
| D． | 两条直线被第三条直线所截，同位角相等 |
4．下列事件中，不确定事件是（ ）
| A． | a是实数，且|a|≥0 | B． | $\frac{1}{2}$+$\frac{x-1}{5}$=0不是分式方程 | ||
| C． | 三角形内角和等于360° | D． | a是实数，a0=1 |
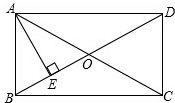在矩形ABCD中，对角线AC、BD交于点O，AE⊥BD，垂足为E，且AE平分∠BAO．若DO=2，求AB和BC的长度．