题目内容
 如图,P为⊙O外一点,PA切⊙O于A,AB是⊙O的直径,PB交⊙O于C,PA=2cm,PC=1cm,则图中阴影部分的面积S是
如图,P为⊙O外一点,PA切⊙O于A,AB是⊙O的直径,PB交⊙O于C,PA=2cm,PC=1cm,则图中阴影部分的面积S是
- A.

- B.

- C.

- D.

C
分析:连AC,OC,由PA切⊙O于A,AB是⊙O的直径,得到∠PAB=90°,∠ACB=90°,易得Rt△PAC∽Rt△PBA,于是PA2=PC•PB,而PB=4,所以∠B=30°,AB=2 cm,三角形OAC为等边三角形.S阴影部分=S△PAC-S弓形AC=S△PAC-(S扇形OAC-S△OAC),分别运用扇形的面积公式和三角形的面积公式进行计算即可.
cm,三角形OAC为等边三角形.S阴影部分=S△PAC-S弓形AC=S△PAC-(S扇形OAC-S△OAC),分别运用扇形的面积公式和三角形的面积公式进行计算即可.
解答: 解:连AC,OC,如图,
解:连AC,OC,如图,
∵PA切⊙O于A,AB是⊙O的直径,
∴∠PAB=90°,∠ACB=90°,
∴Rt△PAC∽Rt△PBA,
∴PA2=PC•PB,
而PA=2cm,PC=1cm,
∴PB=4,
∴∠B=30°,AB=2 cm,
cm,
∴∠AOC=60°,AC=OA= cm,
cm,
∴S阴影部分=S△PAC-S弓形AC,
=S△PAC-(S扇形OAC-S△OAC),
= ×
× ×1-
×1- +
+ ×(
×( )2,
)2,
= cm2.
cm2.
故选C.
点评:本题考查了扇形的面积公式:S= ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.同时考查了切线的性质以及含30度的直角三角形三边的关系.
lR,l为扇形的弧长,R为半径.同时考查了切线的性质以及含30度的直角三角形三边的关系.
分析:连AC,OC,由PA切⊙O于A,AB是⊙O的直径,得到∠PAB=90°,∠ACB=90°,易得Rt△PAC∽Rt△PBA,于是PA2=PC•PB,而PB=4,所以∠B=30°,AB=2
 cm,三角形OAC为等边三角形.S阴影部分=S△PAC-S弓形AC=S△PAC-(S扇形OAC-S△OAC),分别运用扇形的面积公式和三角形的面积公式进行计算即可.
cm,三角形OAC为等边三角形.S阴影部分=S△PAC-S弓形AC=S△PAC-(S扇形OAC-S△OAC),分别运用扇形的面积公式和三角形的面积公式进行计算即可.解答:
 解:连AC,OC,如图,
解:连AC,OC,如图,∵PA切⊙O于A,AB是⊙O的直径,
∴∠PAB=90°,∠ACB=90°,
∴Rt△PAC∽Rt△PBA,
∴PA2=PC•PB,
而PA=2cm,PC=1cm,
∴PB=4,
∴∠B=30°,AB=2
 cm,
cm,∴∠AOC=60°,AC=OA=
 cm,
cm,∴S阴影部分=S△PAC-S弓形AC,
=S△PAC-(S扇形OAC-S△OAC),
=
 ×
× ×1-
×1- +
+ ×(
×( )2,
)2,=
 cm2.
cm2.故选C.
点评:本题考查了扇形的面积公式:S=
 ,其中n为扇形的圆心角的度数,R为圆的半径),或S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S= lR,l为扇形的弧长,R为半径.同时考查了切线的性质以及含30度的直角三角形三边的关系.
lR,l为扇形的弧长,R为半径.同时考查了切线的性质以及含30度的直角三角形三边的关系. 
练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
 10、如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
10、如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )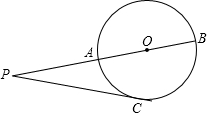 已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R=
已知如图,P为⊙O外一点,过点P作⊙O的切线,切点为C,过P,O两点作⊙O的割线交⊙O于A、B两点,且PC=4cm,PA=3cm,则⊙O的半径R= 如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则
如图,P为圆外一点,PA切圆于A,PA=8,直线PCB交圆于C、B,且PC=4,连接AB、AC,∠ABC=α,∠ACB=β,则 如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO=
如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO= 如图,P为⊙O外一点,过点P作⊙O的两条割线,分别交⊙O于A、B和C、D,且AB为⊙O的直径,已知PA=AO=2cm,弧AC=弧CD,则PC的长为( )
如图,P为⊙O外一点,过点P作⊙O的两条割线,分别交⊙O于A、B和C、D,且AB为⊙O的直径,已知PA=AO=2cm,弧AC=弧CD,则PC的长为( )