题目内容
已知抛物线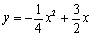 .
.
(Ⅰ)求它的对称轴与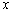 轴交点
轴交点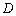 的坐标;
的坐标;
(Ⅱ)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与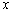 轴的交点为
轴的交点为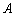 ,
,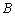 ,与
,与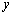 轴的交点为
轴的交点为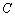 ,若
,若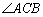 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(Ⅲ)若点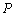 (
(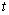 ,
,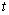 )在抛物线上,则称点
)在抛物线上,则称点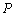 为
为 抛物线的
抛物线的 不动点.将抛物线
不动点.将抛物线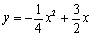 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线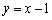 上,请说明理由.
上,请说明理由.
提示:如图,作 ∥
∥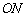 交
交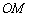 于点
于点 ,作
,作 交
交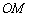 于点
于点 ,
, ,
, 即为所求)
即为所求)

 ∴
∴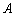
 ,
,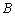
 .
.
∴ .
.

 .
.
∵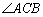 =90°,
=90°,
∴ .
.
即 .
. .
.
解得 ,
, (舍去). …………………………7分
(舍去). …………………………7分
∴抛物线的解析式为 . …………………………8分
. …………………………8分
(Ⅲ)设平移后的抛物线的解析式为 ,
,
由不动点的定义,得方程 , [来源:学科网]
, [来源:学科网]
整理,得 .
.
∵平移后的抛物线只有一个不动点,
∴此方程有两个相等的实数根.
∴判别式 , …………………………9分
, …………………………9分
有 ,
, .
.
∴顶点( ,
, )在直线
)在直线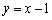 上.
上.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
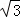 MN.
MN.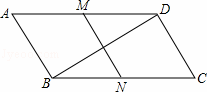
 过点(0,0),(1,3),求抛物线的解析式,并求出抛物线的顶点坐标.
过点(0,0),(1,3),求抛物线的解析式,并求出抛物线的顶点坐标. 正方体 B.
正方体 B.  圆柱 C.
圆柱 C.  圆锥 D.
圆锥 D.  球
球

 B.
B. C.
C. D.
D. 