Question

【题目】如图，某地有一座圆弧形的拱桥，桥下水面宽为7.2m，拱顶高出水面2.4m，现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．

Answer 1

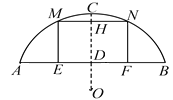
【答案】货船能顺利通过这座拱桥，理由见解析.

【解析】试题分析：根据题意画出图形，利用垂径定理和勾股定理求出拱桥的半径长，连接ON，OA，通过求距离水面2米高处即HD长为2时，桥有多宽即MN的长与货船顶部的3米做比较来判定货船能否通过（MN大于3则能通过，MN小于等于3则不能通过）．先根据半弦，半径和弦心距构造直角三角形求出半径的长，再根据Rt△OHN中勾股定理求出HN的长，从而求得MN的长．

试题解析：如图，连接ON，OA，

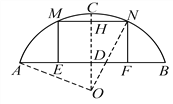
∵OC⊥AB，

∴D为AB中点，

∵AB=7.2m，

∴AD=AB=3.6m．

又∵CD=2.4m，

设OA=OC=ON=r，则OD=（r-2.4）m，

在Rt△AOD中，根据勾股定理得：r2=（r-2.4）2+3.62，解得r=3.9，

∵CD=2.4m，船舱顶部为正方形并高出水面AB=2m，

∴CH=2.4-2=0.4（m），

∴OH=r-CH=3.9-0.4=3.5（m），

在Rt△OHN中，HN2=ON2-OH2=3.92-3.52=2.96（m2），

∴HN=（m），

∴MN=2EN=2×≈3.44m＞3m，

∴此货船能顺利通过这座拱桥．