题目内容
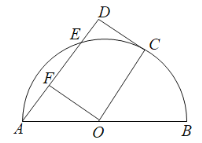
【题目】如图,△ABC中,P'是边AB上一点,四边形P'Q'M'N'是正方形,点Q',![]() 在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
在边BC上,点N'在△ABC内.连接BN',并延长交AC于点N,NM⊥BC于点M,NP⊥MN交AB于点P,PQ⊥BC于点Q.
(1)求证:四边形PQMN为正方形;
(2)若∠A=90°,AC=1.5m,△ABC的面积=1.5m2.求PN的长.
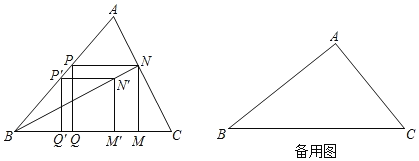
【答案】(1)证明见解析;(2)PN的长为![]() m.
m.
【解析】
(1)先证得四边形PQMN为矩形.根据正方形的性质得到PN∥P'N',MN∥M'N',得到![]() ,
,![]() ,由此证得PN=MN,即可得到结论;
,由此证得PN=MN,即可得到结论;
(2)作AD⊥BC于D,AD交PN于E,根据△ABC的面积=1.5m2求出AB=2,BC=2.5,AD=![]() ,设PN=x,则PQ=DE=x,AE
,设PN=x,则PQ=DE=x,AE![]() x,由PN∥BC证得△APN∽△ABC,即可求出PN.
x,由PN∥BC证得△APN∽△ABC,即可求出PN.
(1)∵NM⊥BC,NP⊥MN,PQ⊥BC,
∴四边形PQMN为矩形.
∵四边形P'Q'M'N'是正方形,
∴PN∥P'N',
∴![]() ,
,
∵MN∥M'N',
∴![]() ,
,
∴![]() ,
,
而P'N'=M'N',
∴PN=MN,
∴四边形PQMN为正方形;
(2)作AD⊥BC于D,AD交PN于E,如图,
∵△ABC的面积=1.5,
∴![]() ABAC=1.5,
ABAC=1.5,
∴AB=2,
∴BC![]() 2.5.
2.5.
∵![]() BCAD=1.5,
BCAD=1.5,
∴AD![]() ,
,
设PN=x,则PQ=DE=x,AE![]() x.
x.
∵PN∥BC,
∴△APN∽△ABC,
∴![]() ,即
,即 ,
,
解得:x![]() ,
,
即PN的长为![]() m.
m.


练习册系列答案
相关题目