题目内容
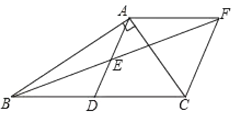
【题目】如图在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形;
是菱形;
(3)若![]() ,求菱形
,求菱形![]() 的面积.
的面积.
【答案】(1)见解析 (2)见解析 (3)10
【解析】
(1)根据AAS求证![]() ;
;
(2)利用(1)中全等三角形的对应边相等得到AF=BD,再结合已知条件,利用“有一组对边平行且相等得四边形是平行四边形”得到四边形![]() 是平行四边形,再根据“直角三角形斜边中线等于斜边的一半”得到
是平行四边形,再根据“直角三角形斜边中线等于斜边的一半”得到![]() ,从而得出结论.
,从而得出结论.
(3)连接![]() ,可得四边形
,可得四边形![]() 是平行四边形,可得到菱形两条对角线的长度,即可求出面积.
是平行四边形,可得到菱形两条对角线的长度,即可求出面积.
解:![]() 证明:
证明:![]()
![]()
![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 边上的中线
边上的中线
![]()
在![]() 和
和![]() 中
中
![]()
![]() 证明:由
证明:由![]() 知
知![]()
则![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]() 是
是![]() 的中点
的中点
![]()
![]() 四边形
四边形![]() 是菱形
是菱形
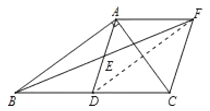
![]() 连接
连接![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]() 四边形
四边形![]() 是菱形
是菱形
![]()
![]()
故答案为:(1)见解析;(2)见解析;(3)10.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目






