题目内容
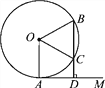
【题目】如图，在△ABC中，∠C=90°，AC=3cm，BC=4cm. P、Q分别为AB、BC上的动点，点P从点A出发沿AB方向作匀速移动的同时，点Q从点B出发沿BC方向向点C作匀速移动，移动的速度均为1cm/s，设P、Q移动的时间为t（0＜t≤4）.
（1）当t为何值时，△BPQ与△ABC相似；
（2）当t为何值时，△BPQ是等腰三角形.
【答案】（1）t=
或
时，△BPQ与△ABC相似；（2）t=2.5或
或
.
【解析】试题分析：
（1）由已知条件易得AB=5，由于△BPQ和△ABC有公共角∠B，所以当
或
时，两三角形相似，由此可列出方程解得t的值；
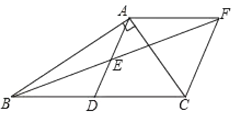
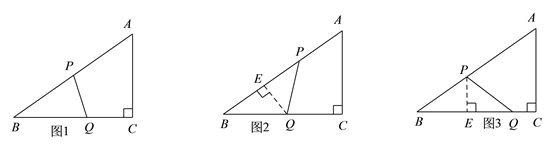
（2）如图，由题意可知，需分三种情况讨论：①BP=BQ时，可直接列方程
求得t的值；②BQ=PQ时，过点Q作QE⊥AB于点E，再证△BQE∽△BAC，从而可利用相似三角形的性质列比例式求出此时t的值；③PB=PQ时，过点P作PE⊥BC于点E，再证△PBE∽△ABC，从而可利用相似三角形的性质列比例式求出此时t的值.
试题解析：
（1）∵在△ABC中，∠C=90°，AC=3cm，BC=4cm.
∴AB=
（cm）.
∵△BPQ和△ABC有公共角∠B，
∴①当
时，△BPQ∽△BCA，由此可得： 
，解得： 
；
②当
时，△BPQ∽△BAC，由此可得： 
，解得： 
；
∴当
或
时，△BPQ与△ABC相似；
（2）①如图1，当BP=BQ时，△BPQ是等腰三角形，由题意可得： 
，解得： 
；
②如图2，当BQ=PQ时，过点Q作QE⊥AB于点E，则BE=PE=
BP=
，∠BEQ=∠C=90°，
又∵∠B=∠B，
∴△BEQ∽△BCA，
∴
，即
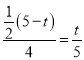，解得： 
；
③如图3，当PB=PQ时，过点P作PE⊥BC于点E，则BE=EQ= 
，∠BEP=∠C=90°，
又∵∠B=∠B，
∴△BEP∽△BCA，
∴
，即
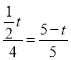，解得： 
；
综上所述，当
， 
， 
时，△BPQ是等腰三角形.
【题目】为了争创全国文明卫生城市，优化城市环境，某市公交公司决定购买10辆全新的混合动力公交车，现有
两种型号，它们的价格及年省油量如下表：
型 号 |
|
|
价格（万元/辆） |
|
|
年省油量（万升/辆） | 2.4 | 2 |
经调查，购买一辆
型车比购买一辆
型车多20万元，购买2辆型车比购买3辆型车少60万元.
（1）请求出
和
的值；
（2）若购买这批混合动力公交车（两种车型都要有）， 每年能节省的油量不低于22.4万升，请问有几种购车方案？（不用一一列出）请求出最省钱的购车方案所需的车款.
