Question

【题目】如图，正方形中，，点在上运动(不与重台)，过点作，交于点，求运动到多长时，有最大值，并求出最大值.

Answer 1

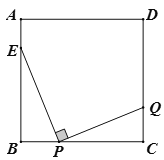
【答案】当BP=6时，CQ最大，且最大值为4.

【解析】

根据正方形的性质和余角的性质可得∠BEP＝∠CPQ，进而可证△BPE∽△CQP，设CQ＝y，BP＝x，根据相似三角形的性质可得y与x的函数关系式，然后利用二次函数的性质即可求出结果．

解：∵四边形ABCD是正方形，∴∠B=∠C=90°，

∴∠BEP+∠BPE＝90°，∵，∴∠QPC+∠BPE＝90°，∴∠BEP＝∠CPQ．

∴△BPE∽△CQP，∴．

设CQ＝y，BP＝x，∵AB=BC=12，∴CP＝12﹣x．∵AE＝AB，AB=12，∴BE＝9，

∴，化简得：y＝﹣（x2﹣12x），即y＝﹣（x﹣6）2+4，

所以当x＝6时，y有最大值为4．即当BP=6时，CQ有最大值，且最大值为4．