如图.四边形ABCD是菱形.对角线AC=8cm.BD=6cm.DH⊥AB于点H.且DH与AC交于G.则GH=( )A．2825cmB．2120cmC．2815cmD．2521cm 题目和参考答案——青夏教育精英家教网—

题目内容

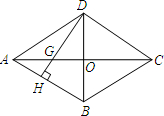（2013•绵阳）如图，四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于点H，且DH与AC交于G，则GH=（　　）

A．

B．

C．

D．

分析：先求出菱形的边长，然后利用面积的两种表示方法求出DH，在Rt△DHB中求出BH，然后得出AH，利用tan∠HAG的值，可得出GH的值．

解答：解：∵四边形ABCD是菱形，对角线AC=8cm，BD=6cm，
∴AO=4cm，BO=3cm，
在Rt△AOB中，AB=

AO2+BO2

=5cm，
∵

BD×AC=AB×DH，
∴DH=

cm，
在Rt△DHB中，BH=

DB2-DH2

cm，
则AH=AB-BH=

cm，
∵tan∠HAG=

，
∴GH=

AH=

cm．
故选B．

点评：本题考查了菱形的性质、解直角三角形及三角函数值的知识，注意菱形的面积等于对角线乘积的一半，也等于底乘高．

练习册系列答案

相关题目

（2013•绵阳）如图，已知矩形OABC中，OA=2，AB=4，双曲线y=

（k＞0）与矩形两边AB、BC分别交于E、F．
（1）若E是AB的中点，求F点的坐标；
（2）若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值．

（2013•绵阳）如图，AB是⊙O的直径，C是半圆O上的一点，AC平分∠DAB，AD⊥CD，垂足为D，AD交⊙O于E，连接CE．
（1）判断CD与⊙O的位置关系，并证明你的结论；
（2）若E是

的中点，⊙O的半径为1，求图中阴影部分的面积．

（2013•绵阳）如图，要拧开一个边长为a=6mm的正六边形螺帽，扳手张开的开口b至少为（　　）

（2013•绵阳）如图，在两建筑物之间有一旗杆，高15米，从A点经过旗杆顶点恰好看到矮建筑物的墙角C点，且俯角α为60°，又从A点测得D点的俯角β为30°，若旗杆底点G为BC的中点，则矮建筑物的高CD为（　　）

试题分类