题目内容
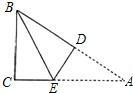如图，在三角形纸片ABC中，AC=6，∠A=30°，∠C=90°，将∠A沿DE折叠，使点A与点B重合，则折痕DE的长为（ ）| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
分析：利用翻折变换及勾股定理的性质．
解答：解：∵∠A=30°，∠C=90°，
∴∠CBD=60°．
∵将∠A沿DE折叠，使点A与点B重合，
∴∠A=∠DBE=∠EBC=30°．
∵∠EBC=∠DBE，∠BCE=∠BDE=90°，BE=BE，
∴△BCE≌△BDE．
∴CE=DE．
∵AC=6，∠A=30°，
∴BC=AC×tan30°=2
．
∵∠CBE=30°．
∴CE=2．即DE=2．
故选D．
∴∠CBD=60°．
∵将∠A沿DE折叠，使点A与点B重合，
∴∠A=∠DBE=∠EBC=30°．
∵∠EBC=∠DBE，∠BCE=∠BDE=90°，BE=BE，
∴△BCE≌△BDE．
∴CE=DE．
∵AC=6，∠A=30°，
∴BC=AC×tan30°=2
| 3 |
∵∠CBE=30°．
∴CE=2．即DE=2．
故选D．
点评：考查了学生运用翻折变换及勾股定理等来综合解直角三角形的能力．
练习册系列答案
相关题目
如图，在三角形纸片ABC中，∠ACB=90°，BC=3，AB=6．在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则CE的长度为（ ）| A、3 | ||
| B、6 | ||
C、
| ||
D、2
|
如图，在三角形纸片ABC中，∠A=65°，∠B=75°，将纸片的一角折叠（折痕为DE），使点C落在△ABC内的C′处，若∠AEC′=20°，则∠BDC′的度数是（ ）| A、30° | B、40° | C、50° | D、60° |
如图，在三角形纸片ABC中，∠ACB=90°，BC=3，AB=6，在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则CE的长度为（ ）
（2012•太原一模）如图，在三角形纸片ABC中，BC=3，AB=5，∠BCA=90°，将其对折后点A落在BC的延长线上，折痕与AC交于点E，则CE的长是（ ）