题目内容
3．计算：（x+y-z）2（z-x-y）3+（z-x-y）（x+y-z）4．分析：x+y-z与z-x-y的关系是互为相反数
故可令x+y-z=A，则z-x-y=-A
解：令x+y-z=A，则z-x-y=-A
原式=A2•（-A）3+（-A）•A4=-A5-A5=-2A5=-2（x+y-z）5．
分析 根据x+y-z与z-x-y可知两个式子中的各项都化为相反数，从而可以得到x+y-z与z-x-y的关系，进而可以解答本题．
解答 解：计算：（x+y-z）2（z-x-y）3+（z-x-y）（x+y-z）4．
分析：x+y-z与z-x-y的关系是 互为相反数
故可令x+y-z=A，则z-x-y=-A
解：令x+y-z=A，则z-x-y=-A
原式=A2•（-A）3+（-A）•A4=-A5-A5=-2A5=-2（x+y-z）5．
故答案为：互为相反数、-A、-A、A2•（-A）3+（-A）•A4、-A5-A5、-2A5、-2（x+y-z）5．
点评 本题考查同底数幂的乘法，解题的关键是找到x+y-z与z-x-y的关系．
练习册系列答案
名校课堂系列答案
相关题目
11．
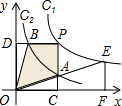如图，两个反比例函数y1=$\frac{{k}_{1}}{x}$（其中k1＞0）和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2，点P在C1上．矩形PCOD交C2于A、B两点，OA的延长线交C1于点E，EF⊥x轴于F点，且图中四边形BOAP的面积为6，则EF：AC为（ ）
如图，两个反比例函数y1=$\frac{{k}_{1}}{x}$（其中k1＞0）和y2=$\frac{3}{x}$在第一象限内的图象依次是C1和C2，点P在C1上．矩形PCOD交C2于A、B两点，OA的延长线交C1于点E，EF⊥x轴于F点，且图中四边形BOAP的面积为6，则EF：AC为（ ）| A． | $\sqrt{3}$﹕1 | B． | 2﹕$\sqrt{3}$ | C． | 2﹕1 | D． | 29﹕14 |
11．已知10a=20，10b=$\frac{1}{5}$，则3a÷3b的值等于（ ）
| A． | 10 | B． | 9 | C． | 8 | D． | 7 |
12．计算（-4a-1）（-4a+1）的结果为（ ）
| A． | 16a2-1 | B． | -8a2-1 | C． | -4a2+1 | D． | -16a2+1 |
