题目内容
已知两条平行线l1、l2之间的距离为6,截线CD分别交l1、l2于C、D两点,一直角的顶点P在线段CD上运动(点P不与点C、D重合),直角的两边分别交l1、l2与A、B两点.
(1)操作发现
如图1,过点P作直线l3∥l1,作PE⊥l1,点E是垂足,过点B作BF⊥l3,点F是垂足.此时,小明认为△PEA∽△PFB,你同意吗?为什么?
(2)猜想论证
将直角∠APB从图1的位置开始,绕点P顺时针旋转,在这一过程中,试观察、猜想:当AE满足什么条件时,以点P、A、B为顶点的三角形是等腰三角形?在图2中画出图形,证明你的猜想.
(3)延伸探究
在(2)的条件下,当截线CD与直线l1所夹的钝角为150°时,设CP=x,试探究:是否存在实数x,使△PAB的边AB的长为4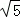 ?请说明理由.
?请说明理由.
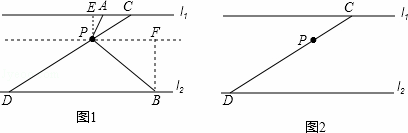


解:(1)如图(1),由题意,得:∠EPA+∠APF=90°,∠FPB+∠APF=90°,
∴∠EPA=∠FPB,
又∵∠PEA=∠PFB=90°,
∴△PEA∽△PFB;
(2)证明:如图2,∵∠APB=90°,
∴要使△PAB为等腰三角形,只能是PA=PB,

当AE=BF时,PA=PB,
∵∠EPA=∠FPB,∠PEA=∠PFB=90°,AE=BF,
∴△PEA≌△PFB,
∴PA=PB;
(3)如图2,在Rt△PEC中,CP=x,∠PCE=30°,
∴PE= x,
x,
由题意,PE+BF=6,BF=AE,
∴AE=6﹣ x,
x,
当AB=4 时,由题意得PA=2
时,由题意得PA=2 ,
,
Rt△PEA中,PE2+AE2=PA2,
即( )2+(6﹣
)2+(6﹣ x)2=40,
x)2=40,
整理得:x2﹣12x﹣8=0,
解得:x=6﹣2 <0(舍去)或x=6+2
<0(舍去)或x=6+2 ,
,
∵x=6+2 >6+6=12,又CD=12,
>6+6=12,又CD=12,
∴点P在CD的延长线上,这与点P在线段CD上运动相矛盾,
∴不合题意,
综上,不存在满足条件的实数x.



参加广安市2014年高中阶段教育学生招生考试的学生大约有4.3万人,将4.3万人用科学记数法表示应为( )
|
| A. | 4.3×104人 | B. | 43×105人 | C. | 0.43×105人 | D. | 4.3×105人 |


 、0.2、
、0.2、 、
、 、
、 、
、 、中,无理数的个数( )
、中,无理数的个数( )

 的解集是
的解集是 
 cm B.
cm B. cm C.
cm C. cm D.
cm D. cm
cm 的直线与
的直线与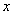 轴平行,且直线分别与反比例函数
轴平行,且直线分别与反比例函数  和
和 的图象交于点
的图象交于点 、点
、点 .
. 的面积为8 ,求k的值 .
的面积为8 ,求k的值 . 
