题目内容
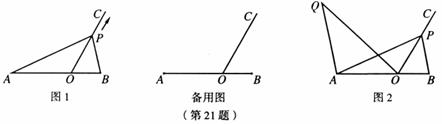
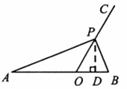
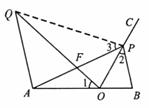
如图1,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t=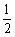 秒时,则OP= ,S△ABP= ;
秒时,则OP= ,S△ABP= ;
(2)当△ABP是直角三角形时,求t的值;
(3)如图2,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B,求证:AQ·BP=3.
解:(1)1,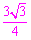 ;
;
(2)①∵∠A<∠BOC=60°,
∴∠A不可能是直角.
②当∠ABP=90°时,
∵∠BOC=60°,
∴∠OPB=30°.
∴OP=2OB,即2t=2.
∴t=1.
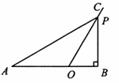
③当∠APB=90°时,作PD⊥AB,垂足为D,则∠ADP=∠PDB=90°.
∵OP=2t,
∴OD=t,PD=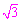 t,AD=2+t,BD=1-t(△BOP是锐角三角形).
t,AD=2+t,BD=1-t(△BOP是锐角三角形).
解法一:∴BP2=(1-t)2 +3t2,AP2=(2+t)2+3t2.
∵BP2+AP2=AB2,
∴(1-t)2+3t2+(2+t)2+3t2=9,
即4t2+t-2=0.
解得t1=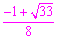 ,t2=
,t2= 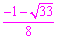 (舍去).
(舍去).
解法二:∵∠APD+∠BPD=90°,∠B+∠BPD=90°,
∴∠APD=∠B.
∴△APD∽△PBD.
∴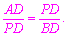
∴PD2=AD·BD.
于是(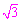 t)2=(2+t)(1-t),即 4t2+t-2=0.
t)2=(2+t)(1-t),即 4t2+t-2=0.
解得t1=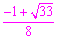 ,t2=
,t2= 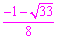 (舍去).
(舍去).
综上,当△ABP为直角三角形时,t=1或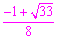 .
.
(3)解法一:∵AP=AB,
∴∠APB=∠B.
作OE∥AP,交BP于点E,
∴∠OEB=∠APB=∠B.
∵AQ∥BP,
∴∠QAB+∠B=180°.
又∵∠3+∠OEB=180°,
∴∠3=∠QAB.
又∵∠AOC=∠2+∠B=∠1+∠QOP,
已知∠B=∠QOP,
∴∠1=∠2.
∴△QAO∽△OEP.
∴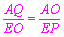 ,即AQ·EP=EO·AO.
,即AQ·EP=EO·AO.
∵OE∥AP,
∴△OBE∽△ABP.
∴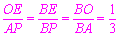 .
.
∴OE=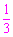 AP=1,BP=
AP=1,BP=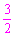 EP.
EP.
∴AQ·BP=AQ·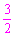 EP=
EP=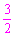 AO·OE=
AO·OE=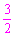 ´2´1=3.
´2´1=3.
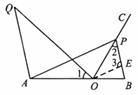
解法二:连接PQ,设AP与OQ相交于点F.
∵AQ∥BP,
∴∠QAP=∠APB.
∵AP=AB,
∴∠APB=∠B.
∴∠QAP=∠B.
又∵∠QOP=∠B,
∴∠QAP=∠QOP.
∵∠QFA=∠PFO,
∴△QFA∽△PFO.
∴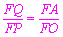 ,即
,即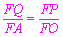 .
.
又∵∠PFQ=∠OFA,
∴△PFQ∽△OFA.
∴∠3=∠1.
∵∠AOC=∠2+∠B=∠1+∠QOP,
已知∠B=∠QOP,
∴∠1=∠2.
∴∠2=∠3.
∴△APQ∽△BPO.
∴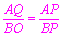 .
.
∴AQ·BP=AP·BO=3´1=3.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案2014年4月21日8时我市区县的可吸人颗粒物数值统计如下表
| 区县 | 曹县 | 单县 | 成武 | 定陶 | 巨野 | 东明 | 郓城 | 鄄城 | 牡丹区 | 开发区 |
| 可吸入颗粒物 (mg/m3) | 0.15 | 0.15 | 0.15 | 0.15 | 0.18 | 0.18 | 0.13 | 0.16 | 0.14 | 0.14 |
该日这一时刻的可吸人颗粒物数值的众数和中位数分别是
A.0.15和0. 14 B.0.18和0.15
C.0. 18和0.14 D.0.15和0.15
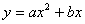 与
与 轴交于点B (-4,0),顶点为(A-2,-4);连接AB,把AB所在直线沿
轴交于点B (-4,0),顶点为(A-2,-4);连接AB,把AB所在直线沿 轴上下平移的直线设为
轴上下平移的直线设为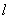 :
: 。
。

 中的
中的 自变量x的取值范围是
自变量x的取值范围是 B.
B. C.
C. D.
D. ,
, 是关于x的一元二次方程
是关于x的一元二次方程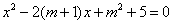 的两实数根.
的两实数根. ,求m的值;
,求m的值;