Question

如图，∠ABC=90°，∠ABC的顶点B在⊙O上，∠ABC的两边交⊙O于D，E两点，BD=4，BE=8，将∠ABC绕点B顺时针旋转30°，∠ABC旋转后的对应边交⊙0于F，G两点，则点D到FG的距离为________．

Answer 1

分析：连接DE，FG，EF，过D作DH⊥FG，由90度的圆周角为直径得到DE为圆的直径，在直角三角形BDE中，由BD与BE的长，利用勾股定理求出DE的长，进而确定出OD的长，再由同弧所对的圆周角等于所对圆心角的一半求出∠EOG的度数，利用对顶角相等得到∠DOH的度数，在直角三角形ODH中，利用锐角三角函数定义及特殊角的三角函数值即可求出DH的长．
解答：解：连接DE，FG，EF，过D作DH⊥FG，如图所示，
∵∠DBE=90°，
∴DE为圆的直径，
在Rt△BDE中，BD=4，BE=8，
∴根据勾股定理得：DE=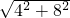=4，即OD=2，
∵∠EBG与∠EOG都为，
∴∠DOH=∠EOG=2∠EBG=60°，
则DH=ODsin60°=2×=．
故答案为：
点评：此题考查了圆周角定理，旋转的性质，以及解直角三角形的性质，熟练掌握圆周角定理是解本题的关键．