题目内容
如图(一),在平面直角坐标系中,射线OA与x轴的正半轴重合,射线OA绕着原点O逆时针到OB位置,把转过的角度记为α,把射线OA称为∠α的始边,射线OB称为∠α的终边、设α是一个任意角,α的终边上任意一点P(除端点外)的坐标是P(x,y),它到原点的距离是 ,那么定义:∠α的正弦
,那么定义:∠α的正弦 ,∠α的余弦
,∠α的余弦 ,∠α的正切
,∠α的正切 .
.根据以上的定义当α=120°时,如图(二)在120°角的终边OB上取一点P(
 ),则
),则 ;
; ,
, ,
,

根据以上所学知识填空:
(1)sin150°=______,cos150°=______
【答案】分析:(1)根据题目中的定义,当α=150°时,在角的终边OB上取一点P,给出其坐标;可得x、y的值,进而可得r的值;根据题目中的定义方法可得答案.
(2)根据(180°-α)与α的终边的关系,得到其上的点的对应关系,进而可得其三角函数间的关系;
(3)同(1);当α=135°时,在角的终边OB上取一点P(-1,1),可得x、y的值,进而可得r的值;根据题目中的定义方法可得答案.
解答:解:(1)根据以上的定义:当α=150°时,在角的终边OB上取一点P(- ,1),则x=-
,1),则x=- ,y=1,则r=2;易得sin150°=
,y=1,则r=2;易得sin150°= ,cos150°=-
,cos150°=- ,tan150°=-
,tan150°=- ;
;
(2)(180°-α)与α的终边关于y轴对称,故其上的点的坐标对应关系为横坐标相反,而横坐标相等;故可得其关系为sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;
(3)同(1);当α=135°时,在角的终边OB上取一点P(-1,1),则x=-1,y=1,则r= ;易得sin135°=
;易得sin135°= ,cos135°=-
,cos135°=- ,tan135°=-1;
,tan135°=-1;
故答案为(1) ,
, ,
, ;(2)sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;
;(2)sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;
(3) ,
, ,-1
,-1
点评:本题考查锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.
(2)根据(180°-α)与α的终边的关系,得到其上的点的对应关系,进而可得其三角函数间的关系;
(3)同(1);当α=135°时,在角的终边OB上取一点P(-1,1),可得x、y的值,进而可得r的值;根据题目中的定义方法可得答案.
解答:解:(1)根据以上的定义:当α=150°时,在角的终边OB上取一点P(-
 ,1),则x=-
,1),则x=- ,y=1,则r=2;易得sin150°=
,y=1,则r=2;易得sin150°= ,cos150°=-
,cos150°=- ,tan150°=-
,tan150°=- ;
;(2)(180°-α)与α的终边关于y轴对称,故其上的点的坐标对应关系为横坐标相反,而横坐标相等;故可得其关系为sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;
(3)同(1);当α=135°时,在角的终边OB上取一点P(-1,1),则x=-1,y=1,则r=
 ;易得sin135°=
;易得sin135°= ,cos135°=-
,cos135°=- ,tan135°=-1;
,tan135°=-1;故答案为(1)
 ,
, ,
, ;(2)sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;
;(2)sin(180°-α)=sinα,cos(180°-α)=-cosα,tan(180°-α)=-tanα;(3)
 ,
, ,-1
,-1点评:本题考查锐角三角函数的概念:在直角三角形中,正弦等于对边比斜边;余弦等于邻边比斜边;正切等于对边比邻边.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
如图取一根长1.2米的匀质木杆,用细绳绑在木杆的中点O处并将其吊起来.
在左侧距离中点30cm处挂一个重10N的物体,为了保持木杆水平,在右侧用一个弹簧秤竖直向下拉.改变弹簧称与中点O的距离(单位:cm),看弹簧秤的示数F(单位:N)有什么变化,小锐在做此活动时,得到下表的数据:
| l/cm | … | 10 | 15 | 20 | 25 | b | … |
| F/N | … | 30 | 20 | a | 12 | 10 | … |
(2)求F与l的函数解析式;
(3)在平面直角坐标系中画出此函数的图象.

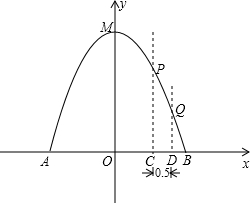 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.




