题目内容
15.已知x=$\frac{1}{2+\sqrt{3}}$,求$\frac{{x}^{2}-4x-2}{x-2}$的值.分析 根据平方差公式,可分母有理化,根据实数的运算,可得答案.
解答 解:x=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}$=2-$\sqrt{3}$.
$\frac{{x}^{2}-4x-2}{x-2}$=x-2=2-$\sqrt{3}$-2=-$\sqrt{3}$.
点评 本题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.

练习册系列答案
相关题目
10.在一年一度的国家学生体质测试中,金星中学对全校2000名男生的1000m测试成绩进行了抽查,学校从初三年级抽取了一部分男生的成绩,并绘制成统计表,绘制成频数直方图.
(1)在这个问题中,总体是什么?
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.

| 序号 | 范围(单位:秒) | 频数 | 频率 |
| 1 | 170<x≤200 | 5 | 0.1 |
| 2 | 200<x≤230 | 13 | a |
| 3 | 230<x≤260 | 15 | 0.3 |
| 4 | 260<x≤290 | c | d |
| 5 | 290<x≤320 | 5 | 0.1 |
| 6 | 320<x≤350 | 2 | 0.04 |
| 7 | 350<x≤380 | 2 | 0.04 |
| 合计 | b | 1.00 |
(2)直接写出a,b,c,d的值.
(3)补全频数直方图.
(4)初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″(即260秒)为合格,你能估计出该校初中男生的1000m的合格人数吗?如果能,请求出合格的人数;如果不能,请说明理由.
4.某班的中考英语口语考试成绩如表:
则该班中考英语口语考试成绩的众数比中位数多1分.
| 考试成绩/分 | 30 | 29 | 28 | 27 | 26 |
| 学生数/人 | 3 | 15 | 13 | 6 | 3 |
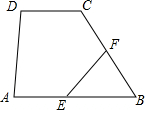 如图所示,在四边形ABCD中,AB∥CD,AD⊥CD,点E、F分别是AB,BC的中点,AB=4,EF=2,∠B=60°,则CD的长为2.
如图所示,在四边形ABCD中,AB∥CD,AD⊥CD,点E、F分别是AB,BC的中点,AB=4,EF=2,∠B=60°,则CD的长为2. 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)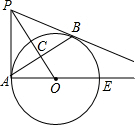 如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.
如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.