题目内容
在△ABC中，I为内心，若∠A=70°，则∠BIC=________．
125°
分析：求出∠ABC+∠ACB的度数，求出∠IBC+∠ICB的度数，根据三角形内角和定理求出即可．
解答：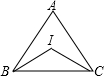
解：∵∠A=70°，
∴∠ABC+∠ACB=180°-∠A=110°，
∵I为内心，
∴∠IBC=
∠ABC，∠ICB=∠ACB，
∴∠IBC+∠ICB=（∠ABC+°，
∴∠BIC=180°-（∠IBC+∠ICB）=125°，
故答案为：125°．
点评：本题考查了三角形的内切圆与内心，三角形的内角和定理的应用，关键是求出∠IBC+∠ICB的度数．
分析：求出∠ABC+∠ACB的度数，求出∠IBC+∠ICB的度数，根据三角形内角和定理求出即可．
解答：
解：∵∠A=70°，∴∠ABC+∠ACB=180°-∠A=110°，
∵I为内心，
∴∠IBC=
∠ABC，∠ICB=∠ACB，∴∠IBC+∠ICB=
（∠ABC+°，∴∠BIC=180°-（∠IBC+∠ICB）=125°，
故答案为：125°．
点评：本题考查了三角形的内切圆与内心，三角形的内角和定理的应用，关键是求出∠IBC+∠ICB的度数．
练习册系列答案
相关题目
如图，在△ABC中，AD为中线，点E、F、G为AD的四等分点，在△ABC内任意抛一粒豆子，豆子落在阴影部分的概率为
