题目内容
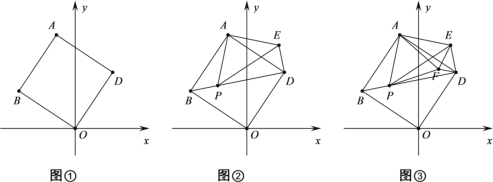
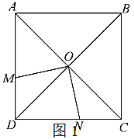
【题目】小明在学完了平行四边形这个章节后,想对“四边形的不稳定性”和“四边形的判定”有更好的理解,做了如下的探究:他将8个木棍和一些钉子组成了一个正方形![]() 和平行四边形
和平行四边形![]() (如图1),且
(如图1),且![]() ,
,![]() 在一条直线上,点
在一条直线上,点![]() 落在边
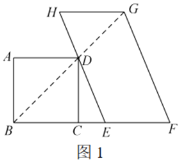
落在边![]() 上.经小明测量,发现此时
上.经小明测量,发现此时![]() 、
、![]() 、
、![]() 三个点在一条直线上,
三个点在一条直线上,![]() ,
,![]() .
.

(1)求![]() 的长度;
的长度;
(2)设![]() 的长度为
的长度为![]() ,
,![]() ________(用含
________(用含![]() 的代数式表示);
的代数式表示);
(3)小明接着探究,在保证![]() ,
,![]() 位置不变的前提条件下,从点
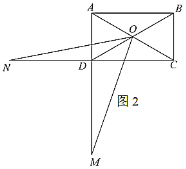
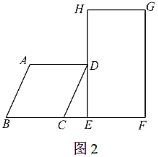
位置不变的前提条件下,从点![]() 向右推动正方形,直到四边形
向右推动正方形,直到四边形![]() 刚好变为矩形时停止推动(如图2).若此时
刚好变为矩形时停止推动(如图2).若此时![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用正方形与平行四边形的性质证明![]() 为等腰三角形可得答案,
为等腰三角形可得答案,
(2)作![]()
![]() 在
在![]() 上,利用等腰直角三角形的性质可得答案,
上,利用等腰直角三角形的性质可得答案,
(3)利用勾股定理求解![]() ,进而求解
,进而求解![]() 从而可得答案.
从而可得答案.
(1)解:![]() 正方形
正方形![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
∴![]() 为等腰三角形
为等腰三角形
∴![]()
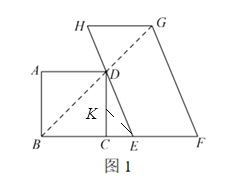
(2)如图,作![]()
![]() 在
在![]() 上,
上,
则![]()
![]() 平行四边形
平行四边形![]()
![]()
![]()
![]()
![]()
设![]()
![]()
![]()
![]()
故答案为:![]()
(3)由于在推动过程中![]() 的长度保持不变,
的长度保持不变,
∴![]()
∴![]() 中,由勾股定理可得
中,由勾股定理可得
![]()
∴![]()
![]() ,又
,又![]() ,∴
,∴![]() ,
,
![]()
![]() (负根舍去)
(负根舍去)
∴![]() .
.


练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目