题目内容
10．
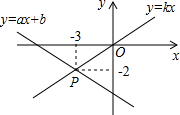如图，函数y=ax+b和y=kx的图象交于点P，则根据图象可知二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是（ ）| A． | $\left\{\begin{array}{l}x=-2\\ y=-3\end{array}\right.$ | B． | $\left\{\begin{array}{l}x=-3\\ y=-2\end{array}\right.$ | C． | $\left\{\begin{array}{l}x=0\\ y=-3\end{array}\right.$ | D． | $\left\{\begin{array}{l}x=0\\ y=-2\end{array}\right.$ |
分析 一次函数图象的交点就是两函数组成的方程组的解．
解答 解：∵函数y=ax+b和y=kx的图象交于点P（-3，-2），
∴二元一次方程组$\left\{\begin{array}{l}y=ax+b\\ y=kx\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-3}\\{y=-2}\end{array}\right.$，
故选B
点评 此题主要考查了一次函数与二元一次方程组，关键是掌握二元一次方程（组）与一次函数的关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．已知三个数2，$\sqrt{2}$，4．如果再添加一个数，就得到这四个数成比例了，则添加的数是（ ）
| A． | 2$\sqrt{2}$ | B． | 2$\sqrt{2}$或$\frac{\sqrt{2}}{2}$ | C． | 2$\sqrt{2}$，4$\sqrt{2}$或8$\sqrt{2}$ | D． | 2$\sqrt{2}$，$\frac{\sqrt{2}}{2}$或4$\sqrt{2}$ |
18．下列命题是真命题的是（ ）
| A． | 有一个角相等的两个等腰三角形相似 | |
| B． | 两边对应成比例且有一个角相等的两个三角形相似 | |
| C． | 四个内角都对应相等的两个四边形相似 | |
| D． | 斜边和一条直角边对应成比例的两个直角三角形相似 |
