题目内容
 已知△ABC的内切圆半径为r,∠A=60°,
已知△ABC的内切圆半径为r,∠A=60°,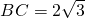 ,则r的取值范围是________.
,则r的取值范围是________.
0<r≤1
分析:首先假设CF的长为x,则BF的长为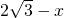 .运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.
.运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.
解答: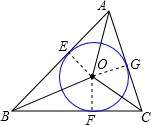 解:方法1:设CF的长为x,则BF的长为
解:方法1:设CF的长为x,则BF的长为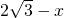 .
.
在Rt△AEO内,AO=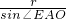 =
=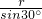 =2r,AE=AO•cos30°=
=2r,AE=AO•cos30°=
∴AC=AG+CG=AE+CF=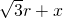 ,AB=AE+BE=
,AB=AE+BE=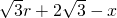
在△ABC中,AB边上的高=AC•sin60°=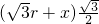
S△ABC=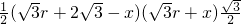
S△ABC=S△ABO+S△BCO+S△ACO=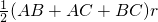 =
=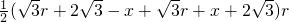
∴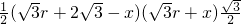 =
=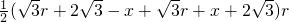
化简得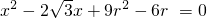
∴△=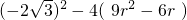 ≥0,即3r2-2r-1≤0
≥0,即3r2-2r-1≤0
解得
结合题意只能是0<r≤1.
方法2:设AB=x,AC=y,
因为S△ABC= AB•AC•sinA=
AB•AC•sinA= (a+b+c)r
(a+b+c)r
代入数据得到r=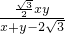 ①
①
又在直角三角形AEO中,AE= r=
r= (x+y-2
(x+y-2 )
)
得到x+y=2 (r+1)xy=2
(r+1)xy=2 y(r+1)-y 2
y(r+1)-y 2
代入①,整理得到关于y的一元二次方程 y2-3(r+1)y+(2
y2-3(r+1)y+(2 r2+4
r2+4 r)=0
r)=0
因为△≥0
得到r2+2r-3≥0
所以-3≤r≤1
结合题意只能是0<r≤1.<R《1
故答案为0<r≤1.
点评:本题考查三角形内切圆与内心、一元二次方程的应用.本题解题的关键是将求r的取值范围转化为一元二次方程,利用判别式△=b2-4ac求解.
分析:首先假设CF的长为x,则BF的长为
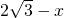 .运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.
.运用∠A=60°用内切圆半径表示AE的长,进而通过x、r表示出AC、AB的长,并表示出△ABC的面积.再将△ABC的面积用三个小三角形面积的和表示出来.这样就建立起了关于x、r的关系式.将关系式看做关于x的一元二次方程判定r的取值范围.结合实际r的最后取值范围即可确定.解答:
 解:方法1:设CF的长为x,则BF的长为
解:方法1:设CF的长为x,则BF的长为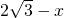 .
.在Rt△AEO内,AO=
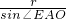 =
=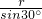 =2r,AE=AO•cos30°=
=2r,AE=AO•cos30°=
∴AC=AG+CG=AE+CF=
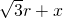 ,AB=AE+BE=
,AB=AE+BE=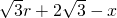
在△ABC中,AB边上的高=AC•sin60°=
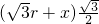
S△ABC=
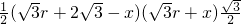
S△ABC=S△ABO+S△BCO+S△ACO=
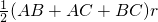 =
=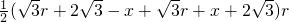
∴
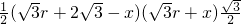 =
=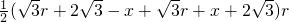
化简得
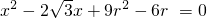
∴△=
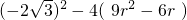 ≥0,即3r2-2r-1≤0
≥0,即3r2-2r-1≤0解得

结合题意只能是0<r≤1.
方法2:设AB=x,AC=y,
因为S△ABC=
 AB•AC•sinA=
AB•AC•sinA= (a+b+c)r
(a+b+c)r代入数据得到r=
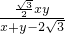 ①
①又在直角三角形AEO中,AE=
 r=
r= (x+y-2
(x+y-2 )
)得到x+y=2
 (r+1)xy=2
(r+1)xy=2 y(r+1)-y 2
y(r+1)-y 2代入①,整理得到关于y的一元二次方程
 y2-3(r+1)y+(2
y2-3(r+1)y+(2 r2+4
r2+4 r)=0
r)=0因为△≥0
得到r2+2r-3≥0
所以-3≤r≤1
结合题意只能是0<r≤1.<R《1
故答案为0<r≤1.
点评:本题考查三角形内切圆与内心、一元二次方程的应用.本题解题的关键是将求r的取值范围转化为一元二次方程,利用判别式△=b2-4ac求解.

练习册系列答案
相关题目
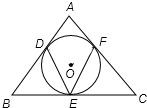 16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( )
16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( ) 已知△ABC的内切圆半径r=
已知△ABC的内切圆半径r= 已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程.
已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程. 如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( )
如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( ) 上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.
上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.