题目内容
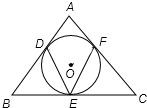
 已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程.
已知△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.试探究∠FDE和∠A之间的关系,并写出推理过程.分析:根据切线性质得出∠AFO=∠AEO=90°,求出∠A=180°-∠FOE,根据圆周角定理得出∠FOE=2∠FDE,代入求出即可.
解答:解:∠A=180°-2∠FDE,理由是:
∵△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.
∴∠AFO=∠AEO=90°,
∴∠A=360°-∠AFO-∠AEO-∠FOE=180°-∠FOE,
∵弧EF对的圆周角是∠EDF,对的圆心角是∠FOE,
∴∠FOE=2∠FDE,
∴∠A=180°-2∠FDE.
∵△ABC的内切圆O与边BC、CA、AB分别相切于点D、E、F.
∴∠AFO=∠AEO=90°,
∴∠A=360°-∠AFO-∠AEO-∠FOE=180°-∠FOE,
∵弧EF对的圆周角是∠EDF,对的圆心角是∠FOE,
∴∠FOE=2∠FDE,
∴∠A=180°-2∠FDE.
点评:本题考查了三角形的内切圆,圆周角定理,切线的性质的应用,关键是得出∠AEO=∠AFO=90°和∠FOE=2∠FDE.

练习册系列答案
相关题目
 16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( )
16、已知△ABC的内切圆⊙O如图,若∠DEF=54°,则∠BAC等于( ) 已知△ABC的内切圆半径r=
已知△ABC的内切圆半径r= 如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( )
如图,已知△ABC的内切圆O与三边分别切于D、E、F,∠A=60°,CB=6cm,△ABC的周长为16cm,则DF的长等于( ) 上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.
上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.