题目内容
 如图,在平面直角坐标系中,A(0,2),B(-1,0),Rt△AOC的面积为4.
如图,在平面直角坐标系中,A(0,2),B(-1,0),Rt△AOC的面积为4.(1)求点C的坐标;
(2)抛物线y=ax2+bx+c经过A、B、C三点,求抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.
考点:二次函数综合题
专题:
分析:(1)由A(0,2),可得OA=2,再由Rt△AOC的面积为4,得OC的值,即可求了C点的坐标,
(2)设抛物线的解析式为:y=ax2+bx+c,把A(0,2),B(-1,0),C(4,0)代入,即可求出抛物线的解析式,可得出对称轴,
(3)由点A,C的坐标,可求出直线AC的解析式,过点P作PQ⊥x轴于H,交直线AC于Q,过点P作PM⊥AC于点M,由OA=2,OC=4,可得AC的值,从而得出cos∠ACO的值,设P(m,n),Q(m,-
m+2),可求出PQ,利用
=
,解得PM,由n=-
m2+
m+2,得PM=
×(-
m2+2m),再由三角形的面积公式即可求出S=-2m2+8m,即可得出当m=2,即P(2,3)时,S的值最大.
(2)设抛物线的解析式为:y=ax2+bx+c,把A(0,2),B(-1,0),C(4,0)代入,即可求出抛物线的解析式,可得出对称轴,
(3)由点A,C的坐标,可求出直线AC的解析式,过点P作PQ⊥x轴于H,交直线AC于Q,过点P作PM⊥AC于点M,由OA=2,OC=4,可得AC的值,从而得出cos∠ACO的值,设P(m,n),Q(m,-
| 1 |
| 2 |
| PM |
| PQ |
2
| ||
| 5 |
| 1 |
| 2 |
| 3 |
| 2 |
2
| ||
| 5 |
| 1 |
| 2 |
解答:解:(1)∵A(0,2),
∴OA=2,
∵Rt△AOC的面积为4,
∴
OC×2=4,解得OC=4,
∴C(4,0),
(2)设抛物线的解析式为:y=ax2+bx+c,
把A(0,2),B(-1,0),C(4,0)代入,得
,
解得
.
所以抛物线的解析式为:y=-
x2+
x+2,对称轴为:x=
,
(3)设直线AC的解析式为:y=kx+b,代入点A(0,2),C(4,0),得:
,
解得
.
∴直线AC的解析式为:y=-
x+2,
过点P作PQ⊥x轴于H,交直线AC于Q,过点P作PM⊥AC于点M,

∵OA=2,OC=4,
∴AC=
=2
,
∴cos∠ACO=
=
,
∵设P(m,n),Q(m,-
m+2),
∴PQ=n+
m-2,
∴
=
=
,
解得PM=
×(n+
m-2),
∵n=-
m2+
m+2
PM=
×(n+
m-2)=
×(-
m2+
m+2+
m-2)=
×(-
m2+2m),
∴S=2
×
×(-
m2+2m)=-2m2+8m,
∴S=-2(m-2)2+8,
∴当m=2,即P(2,3)时,S的值最大.
∴OA=2,
∵Rt△AOC的面积为4,
∴
| 1 |
| 2 |
∴C(4,0),
(2)设抛物线的解析式为:y=ax2+bx+c,
把A(0,2),B(-1,0),C(4,0)代入,得
|
解得
|
所以抛物线的解析式为:y=-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
(3)设直线AC的解析式为:y=kx+b,代入点A(0,2),C(4,0),得:
|
解得
|
∴直线AC的解析式为:y=-
| 1 |
| 2 |
过点P作PQ⊥x轴于H,交直线AC于Q,过点P作PM⊥AC于点M,

∵OA=2,OC=4,
∴AC=
| 22+42 |
| 5 |
∴cos∠ACO=
| 4 | ||
2
|
2
| ||
| 5 |
∵设P(m,n),Q(m,-
| 1 |
| 2 |
∴PQ=n+
| 1 |
| 2 |
∴
| PM |
| PQ |
| PM | ||
n+
|
2
| ||
| 5 |
解得PM=
2
| ||
| 5 |
| 1 |
| 2 |
∵n=-
| 1 |
| 2 |
| 3 |
| 2 |
PM=
2
| ||
| 5 |
| 1 |
| 2 |
2
| ||
| 5 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
2
| ||
| 5 |
| 1 |
| 2 |
∴S=2
| 5 |
2
| ||
| 5 |
| 1 |
| 2 |
∴S=-2(m-2)2+8,
∴当m=2,即P(2,3)时,S的值最大.
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2012年张掖市政府投资2亿元人民币建设了廉租房8万平方米,预计2014年投资9.5亿元人民币建设廉租房,若在这两年内每年投资的增长率相同.设每年市政府投资的增长率为x,根据题意,列出方程为( )
| A、2(1+x)2=9.5 |
| B、2(1+x)+2(1+x)2=9.5 |
| C、2+2(1+x)+2(1+x)2=9.5 |
| D、2(1+x)=9.5 |
 如图,点A、B、C在⊙O上,∠ACB=30°,则cos∠AOB的值是( )
如图,点A、B、C在⊙O上,∠ACB=30°,则cos∠AOB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
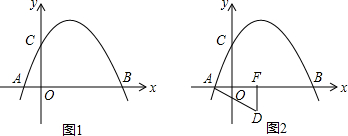
 如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB.延长DA与⊙O的另一个交点为E,连结AC,CE.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB.延长DA与⊙O的另一个交点为E,连结AC,CE. 计算机中的堆栈是一些连续的存储单元,在每个堆栈中数据的存入、取出,按照“先进后出”的原则.如图堆栈(1)的2个连续存储单元已依次存入数据b,a,取出数据的顺序是a,b;堆栈(2)的3个连续存储单元已依次存入数据e、d、c,取出数据的顺序则是c、d、e.现在要从这两个堆栈中取出这5个数据(每次取出1个数据),则不同顺序的取法的种数有
计算机中的堆栈是一些连续的存储单元,在每个堆栈中数据的存入、取出,按照“先进后出”的原则.如图堆栈(1)的2个连续存储单元已依次存入数据b,a,取出数据的顺序是a,b;堆栈(2)的3个连续存储单元已依次存入数据e、d、c,取出数据的顺序则是c、d、e.现在要从这两个堆栈中取出这5个数据(每次取出1个数据),则不同顺序的取法的种数有