题目内容
矩形ABCD的两条对角线相交于点O，∠AOB=60°，AB=4，则矩形的对角线长为________．
8
分析：根据矩形性质得出AO=OC，BO=OD，AC=BD，推出OA=OB，得出△AOB是等边三角形，推出OA=OB=AB=4，即可得出答案．
解答：∵四边形ABCD是矩形，
∴AO=OC，BO=OD，AC=BD，
∴OA=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=4，
∴AC=BD=2AO=8，
故答案为：8．
点评：本题考查了矩形的性质，等边三角形的性质和判定的应用，注意：矩形的对角线相等且互相平分．
分析：根据矩形性质得出AO=OC，BO=OD，AC=BD，推出OA=OB，得出△AOB是等边三角形，推出OA=OB=AB=4，即可得出答案．
解答：∵四边形ABCD是矩形，
∴AO=OC，BO=OD，AC=BD，
∴OA=OB，
∵∠AOB=60°，
∴△AOB是等边三角形，
∴OA=OB=AB=4，
∴AC=BD=2AO=8，
故答案为：8．
点评：本题考查了矩形的性质，等边三角形的性质和判定的应用，注意：矩形的对角线相等且互相平分．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
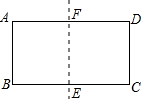如图所示，将矩形ABCD沿两条较长边的中点的连线对折，如果矩形BEFA与矩形ABCD相似，那么AB：AD等于（ ）A、
| ||
B、1：
| ||
C、
| ||
D、1：
|
请将下面证明中每一步的理由填在括号内：
