题目内容
18. 如图,在直角坐标系中,A(0,4),B(-3,0).
如图,在直角坐标系中,A(0,4),B(-3,0).(1)①画出线段AB关于y轴对称线段AC;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)判断四边形ABCD的形状:平行四边形.
(3)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
分析 (1)①根据关于y轴对称的点的横坐标互为相反数确定出点B的位置,然后连接AB即可;
②根据轴对称的性质找出点A关于直线x=3的对称点,即为所求的点D;
(2)对边平行且相等的四边形是平行四边形即可判定四边形ABCD的形状;
(3)根据平行四边形的性质,平分四边形面积的直线经过中心,然后求出AC的中点,代入直线计算即可求出k值.
解答 解:(1)①如图所示;
②直线CD如图所示;
(2)∵由图可知,AD=BC,AD∥BC,
∴四边形ABCD是平行四边形.
故答案为平行四边形.
(3)∵A(0,4),C(3,0),
∴平行四边形ABCD的中心坐标为($\frac{3}{2}$,2),
代入直线得,$\frac{3}{2}$k=2,
解得k=$\frac{4}{3}$.
点评 本题考查了利用旋转变换作图,利用轴对称变换作图,还考查了平行四边形的判定与性质,是基础题,要注意平分四边形面积的直线经过中心的应用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.给出下列命题:①三条线段组成的图形叫三角形 ②相等的角是对顶角;③三角形的角平分线是射线;④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外;⑤任何一个三角形都有三条高、三条中线、三条角平分线;⑥三角形的三条角平分线交于一点,且这点在三角形内.正确的命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.使代数式$\frac{x}{2x-1}$有意义的x的取值范围是( )
| A. | x>$\frac{1}{2}$ | B. | x≠$\frac{1}{2}$ | C. | x≥0且x≠$\frac{1}{2}$ | D. | x≥$\frac{1}{2}$ |
10.下列各式一定成立的是( )
| A. | (2x-y)2=4x2-2xy+y2 | B. | (a-b)2=(b-a)2 | ||
| C. | ($\frac{1}{2}$a-b)2=$\frac{1}{4}$a2+ab+b2 | D. | (x+2y)2=x2+4y2 |
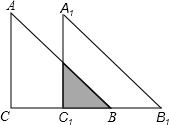 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,