题目内容
等腰三角形的腰长为5,一腰上的高为3,则这个等腰三角形底边的长为________
3或 【解析】分两种情况: (1)顶角是钝角时,如图1所示: 在Rt△ACO中,由勾股定理,得AO2=AC2-OC2=52-32=16, ∴AO=4, OB=AB+AO=5+4=9, 在Rt△BCO中,由勾股定理,得BC2=OB2+OC2=92+32=90, ∴BC=3; (2)顶角是锐角时,如图2所示: 在Rt△ACD中,由勾股定理,得AD2...
练习册系列答案
相关题目
已知二次函数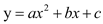 自变量x与函数值y之间满足下列数量关系:
自变量x与函数值y之间满足下列数量关系:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 15 | 8 | 3 | 0 | -1 | 0 | 3 | 8 | 15 |
那么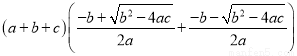 的值为( )
的值为( )
A. -2 B. -1 C. 0 D. 1
A 【解析】根据表中的数据可知,抛物线的对称轴是x=?=1,则?=2.当x=1时,y=a+b+c=?1, 则(a+b+c) =? (a+b+c)=2×(?1)=?2, 故选:A.

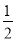 .
.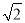 ,x2=﹣
,x2=﹣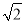
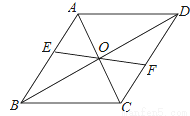
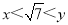 ,则x+y的值是 ________;
,则x+y的值是 ________;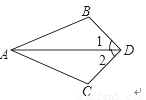
 有四个整数解,则a的取值范围是________________.
有四个整数解,则a的取值范围是________________.