题目内容
3. 已知:如图,在⊙O中,弦AB=$\sqrt{3}$OA,C是$\widehat{AB}$的中点,连接OB,AC和BC,求证:四边形OACB是菱形.
已知:如图,在⊙O中,弦AB=$\sqrt{3}$OA,C是$\widehat{AB}$的中点,连接OB,AC和BC,求证:四边形OACB是菱形.
分析 由C为弧AB的中点,OC为半径,利用垂径定理的逆定理得到PA=PB,OC垂直于AB,由AP为AB的一半,根据题中条件用AO表示出AP,在直角三角形AOP中,利用勾股定理表示出OP,进而确定出OP=PC,即四边形ACBO对角线互相平分,可得出此四边形为平行四边形,再由对角线垂直的平行四边形为菱形即可得证.
解答 证明:∵C为$\widehat{AB}$=的中点,OC为半径,
∴PA=PB,AB⊥OC,
∵AP=$\frac{1}{2}$AB=$\frac{\sqrt{3}}{2}$AO,
∴OP=$\sqrt{A{O}^{2}-A{P}^{2}}$=$\sqrt{A{O}^{2}-\frac{3}{4}A{O}^{2}}$=$\frac{1}{2}$OA=$\frac{1}{2}$OC,
∴PC=$\frac{1}{2}$OC,即OP=PC,
∴四边形OACB是平行四边形,
又∵AB⊥OC,
∴四边形OACB是菱形.
点评 此题考查了垂径定理,勾股定理,菱形的判定,以及平行四边形的判定,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
12.下列各式有意义的条件下不一定成立的是( )
| A. | ${(\sqrt{a})^2}$=a | B. | $\sqrt{a^2}$=a | C. | $\root{3}{a^3}$=a | D. | $\root{3}{{-{a^3}}}$=-a |
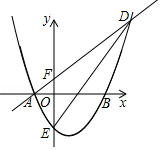 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3).
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)和B(3,0)两点,交y轴于点E(0,-3). 某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题:
某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活情况进行调查统计,并绘制了如图所示的统计表,根据统计图提供的信息解决下列问题: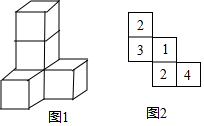 画图题:
画图题: