题目内容
4.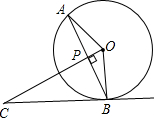 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的切线交OP的延长线于点C.(1)求证:△PBC是等腰三角形;
(2)若⊙O的半径为$\sqrt{5}$,OP=1,求BC的长.
分析 (1)由BC是⊙O的切线,根据切线的性质得到∠OBA+∠ABC=90°,由垂直的定义得到∠OPA+∠A=90°,等量代换得到∠A=∠OBA,∠ABC=∠OPA=∠CPB,进一步得到结果.
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到($\sqrt{5}$)2+x2=(x+1)2,然后解方程即可.
解答 (1)证明:
∵BC是⊙O的切线,
∴∠OBA+∠ABC=90°.
∵OP⊥OA,
∴∠OPA+∠A=90°.
又∵OB=OA,
∴∠A=∠OBA.
∴∠ABC=∠OPA=∠CPB,
∴CP=CB;
∴△PBC是等腰三角形;
(2)解:设BC=x,则PC=x,
在Rt△OBC中,OB=$\sqrt{5}$,OC=CP+OP=x+1,
∵OB2+BC2=OC2,
∴($\sqrt{5}$)2+x2=(x+1)2,
解得x=2,
即BC的长为2.
点评 本题考查了切线的性质、等腰三角形的性质、直角三角形的性质、勾股定理等知识的综合应用,考点较多,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.
如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.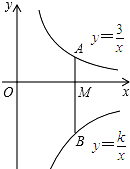 如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.
如图,点A在函数y=$\frac{3}{x}$(x>0)的图象上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,连接AB,AB垂直x轴于点M,且AM:MB=1:2,则k=-6.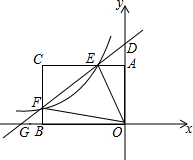 如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(-4,0),C(-4,3)动点F在BC上(不与B、C重合)过点F的反比例函数y=$\frac{k}{x}$的图象与边AB交于点E,直线EF分别与y轴和x轴相交于点D,G
如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(-4,0),C(-4,3)动点F在BC上(不与B、C重合)过点F的反比例函数y=$\frac{k}{x}$的图象与边AB交于点E,直线EF分别与y轴和x轴相交于点D,G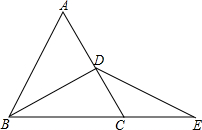 已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E.
已知:如图,在等边三角形ABC的AC边上取中点D,BC的延长线上取一点E,使CE=CD,试说明:∠DBC=∠E. 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.