题目内容
 菱形ABCD的内切圆O与各边分别切于E、F、G、H,在EF与GH上分别作⊙O的切线交AB于M,交BC于N,交CD于P,交DA于Q.求证:MQ∥NP.
菱形ABCD的内切圆O与各边分别切于E、F、G、H,在EF与GH上分别作⊙O的切线交AB于M,交BC于N,交CD于P,交DA于Q.求证:MQ∥NP.考点:圆的综合题
专题:
分析:要证MQ∥NP,因AB∥DC,故可以考虑证明∠AMQ=∠CPN.现∠BAD=∠BCD,故可证△AMQ∽△CPN.于是要证明AM:AQ=CP:CN,进而得出答案.
解答: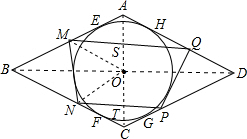 证明:连接MO,NO,BD,AC,
证明:连接MO,NO,BD,AC,
设∠ABC=2α,∠BNM=2β,∠BMN=2γ.则
由ON平分∠ONM,得∠ONC=∠ONM=
(180°-2β)=90°-β;
同理,∠OMN=∠OMA=90°-γ.
而∠CON=180°-∠OCN-∠ONC=β+α=90°-γ,
∵∠BAD=∠BCD,
∴∠OCN=∠MAO
∴△CON∽△AMO,
∴AM:AO=CO:CN,即AM•CN=AO2.
同理,AQ•CP=AO2,
∴AM•CN=AQ•CP,
∴
=
,
∵∠BAD=∠BCD,
∴△AMQ∽△CPN,
∴∠AMQ=∠CPN,
又∵∠BAC=∠DAC=∠BCA=∠ACD,
∴∠ASM=∠NTM,
∴∠ASM=∠ATN,
∴MQ∥NP.
 证明:连接MO,NO,BD,AC,
证明:连接MO,NO,BD,AC,设∠ABC=2α,∠BNM=2β,∠BMN=2γ.则
由ON平分∠ONM,得∠ONC=∠ONM=
| 1 |
| 2 |
同理,∠OMN=∠OMA=90°-γ.
而∠CON=180°-∠OCN-∠ONC=β+α=90°-γ,
∵∠BAD=∠BCD,
∴∠OCN=∠MAO
∴△CON∽△AMO,
∴AM:AO=CO:CN,即AM•CN=AO2.
同理,AQ•CP=AO2,
∴AM•CN=AQ•CP,
∴
| AM |
| CP |
| AQ |
| CN |
∵∠BAD=∠BCD,
∴△AMQ∽△CPN,
∴∠AMQ=∠CPN,
又∵∠BAC=∠DAC=∠BCA=∠ACD,
∴∠ASM=∠NTM,
∴∠ASM=∠ATN,
∴MQ∥NP.
点评:本题考查了菱形的内切圆和三角形的相似以及平行线的判定与性质等知识,根据已知得出△AMQ∽△CPN是解题关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图⊙O′和⊙O″外切于点A,外公切线BC与⊙O′,⊙O″分别切于点B、C,与连心线O′O″交于P,若∠BPO′=30°,则⊙O′与⊙O″的半径的比为( )
如图⊙O′和⊙O″外切于点A,外公切线BC与⊙O′,⊙O″分别切于点B、C,与连心线O′O″交于P,若∠BPO′=30°,则⊙O′与⊙O″的半径的比为( )| A、1:2 | B、1:3 |
| C、2:3 | D、3:4 |
函数y=
的自变量x的取值范围是( )
| x-2 |
| A、x为任意实数 | B、x≤2 |
| C、x≥2 | D、x>2 |
 已知:如图,边长为6的正△ABC内有一边长为4的内接正△DEF,则下列结论①△DBF≌△ECD;②△AEF的周长为10;③△AEF的内切圆的半径为
已知:如图,边长为6的正△ABC内有一边长为4的内接正△DEF,则下列结论①△DBF≌△ECD;②△AEF的周长为10;③△AEF的内切圆的半径为
 已知:二次函数y=ax2+2ax的图象与x轴负半轴的交点为A,将点A绕坐标原点O顺时针旋转120°后得点B.
已知:二次函数y=ax2+2ax的图象与x轴负半轴的交点为A,将点A绕坐标原点O顺时针旋转120°后得点B.