题目内容
关于二次函数y=ax2+bx+c,当x=1时,y=a+b+c可表示为f(1)=a+b+c.已知二次函数f(x)=2x2+9x+34,当任意实数x1≠x2时,有f(x1)=f(x2),则f(x1+x2)= .
考点:二次函数图象上点的坐标特征
专题:新定义
分析:根据f(x1)=f(x2)得到2x12+9x1+34=2x22+9x2+34,整理得到(x1-x2)(2x1+2x2+9)=0,由于x1≠x2,则x1+x2=-
,然后把x=-
代入f(x)=2x2+9x+34中进行计算即可.
| 9 |
| 2 |
| 9 |
| 2 |
解答:解:∵f(x1)=f(x2),
∴2x12+9x1+34=2x22+9x2+34,
∴2x12+9x1-2x22-9x2=0,
∴(x1-x2)(2x1+2x2+9)=0,
∵x1≠x2,
∴2x1+2x2+9=0,
∴x1+x2=-
,
∴f(x1+x2)=f(-
)=2×(-
)2+9×(-
)+34=34.
故答案为34.
∴2x12+9x1+34=2x22+9x2+34,
∴2x12+9x1-2x22-9x2=0,
∴(x1-x2)(2x1+2x2+9)=0,
∵x1≠x2,
∴2x1+2x2+9=0,
∴x1+x2=-
| 9 |
| 2 |
∴f(x1+x2)=f(-
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
故答案为34.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,⊙O直径AB=8,∠CBD=30°,则CD=( )
如图,⊙O直径AB=8,∠CBD=30°,则CD=( )| A、4 | ||
| B、6 | ||
| C、3 | ||
D、2
|
二次函数y=x2-4x+3的图象与x轴的交点坐标是( )
| A、(1,0),(-3,0) |
| B、(1,0),(3,0) |
| C、(-1,0),(-3,0) |
| D、(3,0),(-1,0) |
下列运算中,正确的是( )
| A、a2+a2=a4 |
| B、(a-b)2=a2-b2 |
| C、-a(1-a)=a2-a |
| D、a3•a-4=a-12 |
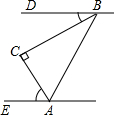 如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )
如图,在△ABC中,∠C=90°,若BD∥AE,∠CAE=70°,则∠DBC的度数是( )| A、20° | B、40° |
| C、50° | D、70° |
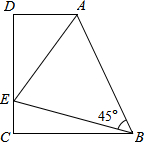 如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度. 如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为
如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为