题目内容
若抛物线y=x2+bx+c与x轴的两个交点坐标分别为（2，0）（4，0），则抛物线的对称轴是________．
x=3
分析：将（2，0）与（4，0）代入抛物线y=x2+bx+c，列出方程组求出b，c，再根据对称轴x=-
得出答案．
解答：∵抛物线y=x2+bx+c与x轴的两个交点坐标分别为（2，0）（4，0），
∴
，
解得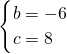
，
∴抛物线的解析式为y=x2-6x+8，
∴对称轴为x=3，
故答案为x=3．
点评：本题考查了抛物线与x轴的交点问题，二次函数图象上点的坐标特征，是基础知识要熟练掌握．
分析：将（2，0）与（4，0）代入抛物线y=x2+bx+c，列出方程组求出b，c，再根据对称轴x=-
得出答案．解答：∵抛物线y=x2+bx+c与x轴的两个交点坐标分别为（2，0）（4，0），
∴
，解得
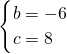，∴抛物线的解析式为y=x2-6x+8，
∴对称轴为x=3，
故答案为x=3．
点评：本题考查了抛物线与x轴的交点问题，二次函数图象上点的坐标特征，是基础知识要熟练掌握．
练习册系列答案
名校课堂系列答案
相关题目
若抛物线y=x2-
x-1与x轴有交点，则k的取值范围是（ ）
| k-1 |
| A、k＞-3 | B、k≥-3 |
| C、k≥1 | D、-3≤k≤1 |