题目内容
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴相交于点A(-3,0),与y轴交于点B,且与正比例函数y=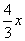 的图象交点为C(m,4)求:
的图象交点为C(m,4)求:
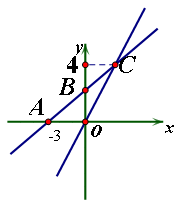
(1)一次函数y=kx+b的解析式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,直接写出点D的坐标.
(3)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
(1)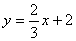 ;
;
(2)(-2,5)或(-5,3).
(3)(5,0)或(-5,0)或(6,0)或(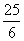 ,0).
,0).
【解析】
分析:(1)首先利用 待定系数法把C(m,4)代入正比例函数y=
待定系数法把C(m,4)代入正比例函数y=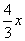 中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
中,计算出m的值,进而得到C点坐标,再利用待定系数法把A、C两点坐标代入一次函数y=kx+b中,计算出k、b的值,进而得到一次函数解析式.
(2)利用△BED1≌△AOB,△BED2≌△AOB,即可得出点D的坐标.
解:(1)∵点C在正比例函数图像上 ∴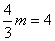 ,
,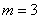
∵点C(3,4)A(—3,0)在一次函数图像上,
∴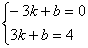
解这个方程组得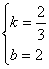
∴一次函数的解析式为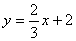
(2)过点D1作D1E⊥y轴于点E,过点D2作D2F⊥x轴于点F,
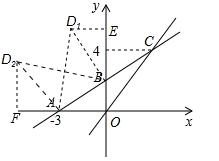
∵点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,∴AB=BD1,
∵∠D1BE+∠ABO=90°,∠ABO+∠BAO=90°,∴∠BAO=∠EBD1,
∵在△BED1和△AOB中,
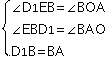
∴△BED1≌△AOB(AAS),
∴BE=AO=3,D1E=BO=2,
即可得出点D的坐标为(-2,5);
同理可得出: △AFD2≌△AOB,
△AFD2≌△AOB,
∴FA=BO=2,D2F=AO=3,
∴点D的坐标为(-5,3).
综上所述:点D的坐标为(-2,5)或(-5,3).
(3)当OC是腰,O是顶角的顶点时,OP=OC=5,则P的坐标是(5,0)或(-5,0);
当OC是腰,C是顶角的顶点时,CP=CO,则P与O关于x=3对称,则P的坐标是(6,0).
当OC是底边时,设P的坐标是(a,0),则
则P的坐标是:(5,0)或(-5,0)或(6,0)或(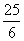 ,0).
,0).
【难度】困难

 阅读快车系列答案
阅读快车系列答案 等于 .
等于 .
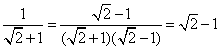 ;
;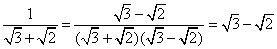 ;
;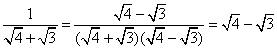 ;
; ;
;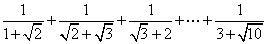 .
. 的图象经过点(a,-a),则a的值为( )
的图象经过点(a,-a),则a的值为( )