题目内容
某中学开展“感恩父母”演讲比赛活动,八(1)、八(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示。
(1)根据下图,分别求出两班复赛的平均成绩和方差;
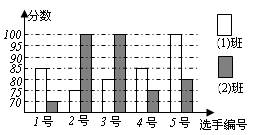
(2)根据(1)的计算结果,哪个班级的复赛成绩较好?为什么?
1)85,70;85,160;(2)八(1).
【解析】
试题分析:(1)从直方图中得到各个选手的得分,由平均数和方差的公式计算;
(2)由方差的意义分析.
试题解析:(1)八(1)班的选手的得分分别为85,75,80,85,100,
∴八(1)班的平均数=(85+75+80+85+100)÷5=85,
八(1)班的方差S12=[(85-85)2+(75-85)2+(80-85)2+(85-85)2+(100-85)2]÷5=70;
八(2)班的选手的得分分别为70,100,100,75,80,
八(2)班平均数=(70+100+100+75+80)÷5=85,
八(2)班的方差S22=[(70-85)2+(100-85)2+(100-85)2+(75-85)2+(80-85)2]÷5=160;
(2)平均数一样的情况下,八(1)班方差小,成绩比较稳定,所以成绩比较好.
【难度】一般

某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行了调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校初中生阅读数学教科书情况统计图表
| 类别 | 人数 | 占总人数比例 |
| 重视 | a | 0.3 |
| 一般 | 57 | 0.38 |
| 不重视 | b | c |
| 说不清楚 | 9 | 0.06 |
(1)求样本容量及表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2300名,请估计该校“不重视阅读数学教科书”的初中人数;
(3)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?




 ”称为二阶行列式,规定它的运算法则为:
”称为二阶行列式,规定它的运算法则为: ,请你根据上述规定求出下列等式中
,请你根据上述规定求出下列等式中 的值.若
的值.若 ,那么
,那么 .
.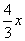 的图象交点为C(m,4)求:
的图象交点为C(m,4)求: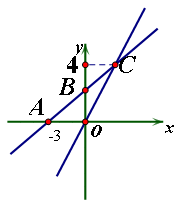


 2的结果是____________ .
2的结果是____________ .