Question

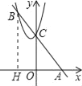
【题目】已知：如图所示，一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点，二次函数y=x2+bx+c的图象过点C，且与一次函数在第二象限交于另一点B，若AC：CB=1：2，那么这二次函数的顶点坐标为_____．

Answer 1

【答案】（﹣，）．

【解析】

由一次函数y=﹣2x+3可求出A、C两点的坐标，再根据B也在此直线上，可设出B点坐标，由AC：CB=1：2可知B点坐标，把B、C点坐标代入二次函数的解析式可求出b、c的值，从而求出其解析式及顶点坐标．

∵一次函数有y=﹣2x+3的图象与x轴、y轴分别交于A、C两点，∴令x=0，得：y=3，令y=0，得：x=，∴A（，0），C（0，3），因为点B在直线y=﹣2x+3的图象上，所以设B点（x，﹣2x+3）．

∵AC：CB=1：2，∴CB=2AC，∴=2，则x2=9，解得：x=3（舍去），x=﹣3，∴x=﹣3．

把B（﹣3，9）C（0，3）代入二次函数解析式得：，解得：，故二次函数的解析式为y=x2+x+3．

∵y=x2+x+3=，故顶点坐标为（﹣）．

故答案为：（﹣）．