题目内容
在某校的平面图上建直角坐标系,以校大门为原点,科技楼的坐标为(5,-12),教学楼坐标为(11,-4),已知科技楼到大门的实际距离为260米,则教学楼到科技楼的距离为 米.
考点:勾股定理的应用
专题:
分析:先画出平面直角坐标系,A、B两点分别表示科技楼、教学楼,则A(5,-12),B(11,-4),利用两点之间的距离公式求出OA=
=13,AB=
=10,再根据科技楼到大门的实际距离为260米,即可求出教学楼到科技楼的距离.
| 52+122 |
| (11-5)2+(-4+12)2 |
解答: 解:如图,A、B两点分别表示科技楼、教学楼,则A(5,-12),B(11,-4).
解:如图,A、B两点分别表示科技楼、教学楼,则A(5,-12),B(11,-4).
∵OA=
=13,AB=
=10,
又科技楼到大门的实际距离为260米,
∴教学楼到科技楼的距离为
×10=200(米).
故答案为200.
 解:如图,A、B两点分别表示科技楼、教学楼,则A(5,-12),B(11,-4).
解:如图,A、B两点分别表示科技楼、教学楼,则A(5,-12),B(11,-4).∵OA=
| 52+122 |
| (11-5)2+(-4+12)2 |
又科技楼到大门的实际距离为260米,
∴教学楼到科技楼的距离为
| 260 |
| 13 |
故答案为200.
点评:本题考查了勾股定理的应用,利用网格结构正确求出OA与AB的长是解题的关键.

练习册系列答案
相关题目
若a<b,则下列各式中,不正确的是( )
| A、a+1<b+1 |
| B、-a<-b |
| C、a-1<b-1 |
| D、2a<2b |
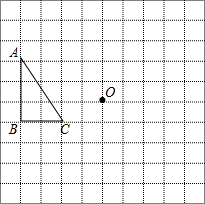 在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上.
在如图的正方形网格中,每个小正方形的边长都是单位1,△ABC的顶点均在格点上. 如图,△ABC沿BC方向平移到△DEF的位置,若BF=8cm,CE=2cm,则平移的距离是
如图,△ABC沿BC方向平移到△DEF的位置,若BF=8cm,CE=2cm,则平移的距离是